Der Unterschied zwischen Effektiv- und Durchschnittsleistung

Antwort: Dies hängt davon ab, wie Sie die Effektivleistung definieren. Sie wollen schließlich nicht den Effektivwert der Wechselstromleistungs-Kurve berechnen, denn das Ergebnis dieser Berechnung hätte keine physikalische Aussagekraft. Dagegen verwenden Sie die Effektivwerte von Spannungen und/oder Strömen zur Berechnung der durchschnittlichen Leistung, was wiederum aussagefähige Resultate ergibt. Diskussion Wie hoch ist die dissipierte Leistung, wenn eine sinusförmige Wechselspannung von 1 VRMS an einen Widerstand von 1 Ω gelegt wird? Dies ist allgemein bekannt1, und somit gibt es hier auch keine Unstimmigkeiten. Wie sieht es aber im Vergleich mit einer Berechnung der Effektivleistung aus? In Bild 1 ist eine sinusförmige Wechselspannung mit einem Effektivwert von 1 V dargestellt. Der Peak-to-Peak-Wert (von Scheitel zu Scheitel) beträgt somit 1 VRMS ∙ 2 ∙ √2 = 2,828 V. Die Spannung schlägt also von -1,414 V bis +1,414 V aus2. 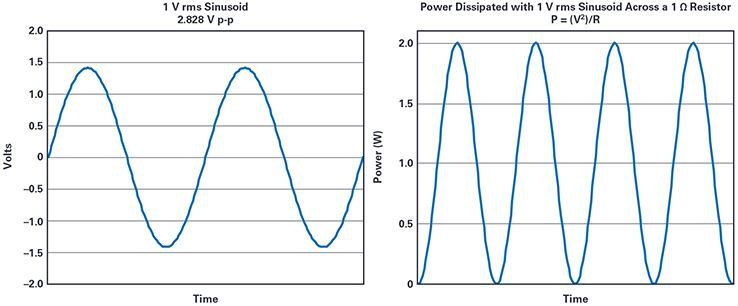Bild 1. Graph einer sinusförmigen Wechselspannung von 1 VRMS. / Bild 2. Verlustleistung an einem 1-Ω-Widerstand bei einer sinusförmigen Wechselspannung von 1 VRMS. Die Kurve in Bild 2 gibt die Leistung wieder, die bei dieser sinusförmigen Spannung von 1 VRMS gemäß der Formel P = V²/R an einem Widerstand von 1 Ω abfällt.

• Die Kurve der Augenblicksleistung weist einen Offset von 1 W auf und schlägt von 0 W bis 2 W aus.
• Der Effektivwert dieser Leistungskurve beträgt 1,225 W.

Eine Möglichkeit zur Berechnung dieses Werts ist Gleichung 2,3: Verifizieren lässt sich dies mit einer detaillierteren Formel4 in MATLAB® oder Excel.

• Der Durchschnittswert dieser Leistungskurve ist dagegen 1 W, was sich einfach visuell herleiten lässt: Die Kurve pendelt symmetrisch um die 1-W-Linie. Durch Berechnung des numerischen Durchschnittswerts der Datenpunkte, die diese Kurve bilden, erhält man dasselbe Resultat.
• Die Durchschnittsleistung entspricht der Leistung, die man bei Verwendung der Effektivspannung erhält.

Die Leistung, die bei einer sinusförmigen Spannung von 1 VRMS an einem Widerstand von 1 Ω abfällt, beträgt also nicht 1,225 W, sondern 1W. Folglich liefert die durchschnittliche Leistung den korrekten Wert, und somit ist auch die durchschnittliche Leistung von physikalischer Relevanz. Die Effektivleistung (nach der hier zugrunde gelegten Definition) hat dagegen keine sinnvolle Bedeutung, ist also von keiner offensichtlichen physikalischen bzw. elektrischen Signifikanz, sondern stellt lediglich eine Größe dar, die man zu Übungszwecken berechnen kann. Eine triviale Übung ist es ebenfalls, die gleiche Analyse mit einem sinusförmigen Strom von 1 ARMS durch einen 1-Ω-Widerstand anzustellen. Das Ergebnis ist das gleiche. Stromversorgungen für integrierte Schaltungen (ICs) liefern in der Regel eine Gleichspannung, weshalb die Effektivleistung bei der Versorgung von ICs kein Thema ist. Bei Gleichstrom sind der Durchschnitts- und der Effektivwert identisch mit dem DC-Wert. Die Verwendung der Durchschnittsleistung anstelle der Effektivleistung nach der in diesem Dokument zugrunde gelegten Definition betrifft stattdessen die Leistung von zeitlich veränderlichen Spannungen und Strömen (z. B. Rauschen, HF-Signale, Oszillatoren). Nutzen Sie die Effektivspannung und den Effektivstrom zur Berechnung der durchschnittlichen Leistung, denn damit erhalten Sie aussagefähige Leistungswerte.

1. Die Leistung, die beim Anlegen einer Spannung an einem Widerstand abfällt, ist eine grundlegende Relation, die sich einfach aus dem ohmschen Gesetz (V = I∙R) sowie den grundlegenden Definitionen von Spannung (Energie pro Ladungseinheit) und Strom (Ladung pro Zeiteinheit) herleiten lässt. Das Produkt aus Spannung und Strom ist somit die Energie pro Zeiteinheit = Leistung.
2. Die Peak-to-Peak-Amplitude einer Sinuswelle ist gleich dem Effektivwert, multipliziert mit 2∙√2 (VP-P = VRMS ∙ 2∙√2). Diese bestens bekannte Beziehung ist in zahllosen Lehrbüchern dokumentiert (unter anderem auch hier: https://de.wikipedia.org/wiki/Quadratisches_Mittel).
3. Dies ist eine Anpassung der Berechnung des Effektivwerts aus einem konstanten DC-Offset zuzüglich eines separaten AC-Effektivwerts und findet sich in der Applikationsschrift „Make Better AC RMS Measurements with Your Digital Multimeter” von Keysight.
4. Die Standarddefinition aus dem Lehrbuch ist ein Beispiel für eine detailliertere Formel:

---

Über den Autor: Doug Ito arbeitet als Applikationsingenieur im High-Speed ADC Team von © Analog Devices, Inc. im kalifornischen San Diego. An der San Diego State University erwarb er ein Bachelor-Diplom in Elektrotechnik. Doug Ito ist Mitglied der EngineerZone® High-Speed ADC Support Community von ADI. Sie erreichen ihn unter douglas.ito@analog.com.