
© Analog Devices Inc.
Application Notes |
Stromrauschen in Verstärkern mit FET-Eingang
Frage: Warum rauscht meine Schaltung bei höheren Frequenzen stärker?
Antwort: Das Phänomen, dass das Stromrauschen mit ansteigender Frequenz zunimmt, ist IC- und Schaltungsentwicklern bekannt. Es war vielen Ingenieuren jedoch nicht zugänglich, weil es entweder zu wenige Fachartikel auf diesem Gebiet gab oder weil die Informationen der Halbleiterhersteller unvollständig waren.
Viele Datenblätter von Halbleiterherstellern, darunter auch diejenigen von ADI, spezifizieren das Stromrauschen eines Verstärkers typischerweise bei einer Frequenz von 1 kHz. Es ist nicht immer klar, wie die aktuellen Rausch-Spezifikationen zustande kommen. Wurden sie gemessen oder theoretisch hergeleitet? Einige Hersteller sind in dieser Hinsicht transparent und geben an, die Spezifikation nach der folgenden Gleichung zu berechnen:
 Diese ist als Schrotrauschen-Gleichung bekannt. Seit jeher spezifiziert ADI die Rauschzahlen seiner meisten Produkte auf diese Weise. Doch gilt dieser berechnete Wert bei allen Verstärkern für Frequenzen bis 1 kHz?
Diese ist als Schrotrauschen-Gleichung bekannt. Seit jeher spezifiziert ADI die Rauschzahlen seiner meisten Produkte auf diese Weise. Doch gilt dieser berechnete Wert bei allen Verstärkern für Frequenzen bis 1 kHz?
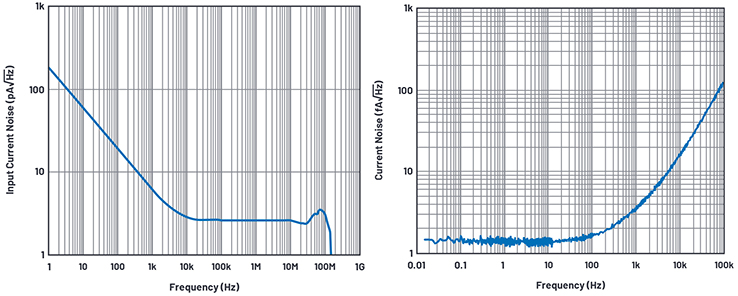 Abbildung 1. Stromrauschen des bipolaren Verstärkers AD8099. / Abbildung 2. Stromrauschen des Verstärkers AD8065 mit FET-Eingang.
In den letzten Jahren interessierte man sich vermehrt für die Frequenzabhängigkeit des Stromrauschens von Verstärkern. Einige Kunden – wie auch Hersteller – gehen davon aus, dass das Stromrauschen von Verstärkern mit FET-Eingang einen ähnlichen Frequenzverlauf aufweist wie das von Verstärkern mit bipolarer Eingangsstufe, das sich z.B. aus einer Flickerrauschkomponente (1/f) und einer flach verlaufenden Breitbandkomponente zusammensetzt (Abbildung 1). Das ist bei Verstärkern mit FET-Eingang jedoch nicht der Fall. Wie aus Abbildung 2 ersichtlich ist, weisen FETs eine bizarr anmutende Rauschcharakteristik auf, über die wenig bekannt ist und die in vielen Simulationsmodellen nicht korrekt abgebildet wird.
Abbildung 1. Stromrauschen des bipolaren Verstärkers AD8099. / Abbildung 2. Stromrauschen des Verstärkers AD8065 mit FET-Eingang.
In den letzten Jahren interessierte man sich vermehrt für die Frequenzabhängigkeit des Stromrauschens von Verstärkern. Einige Kunden – wie auch Hersteller – gehen davon aus, dass das Stromrauschen von Verstärkern mit FET-Eingang einen ähnlichen Frequenzverlauf aufweist wie das von Verstärkern mit bipolarer Eingangsstufe, das sich z.B. aus einer Flickerrauschkomponente (1/f) und einer flach verlaufenden Breitbandkomponente zusammensetzt (Abbildung 1). Das ist bei Verstärkern mit FET-Eingang jedoch nicht der Fall. Wie aus Abbildung 2 ersichtlich ist, weisen FETs eine bizarr anmutende Rauschcharakteristik auf, über die wenig bekannt ist und die in vielen Simulationsmodellen nicht korrekt abgebildet wird.
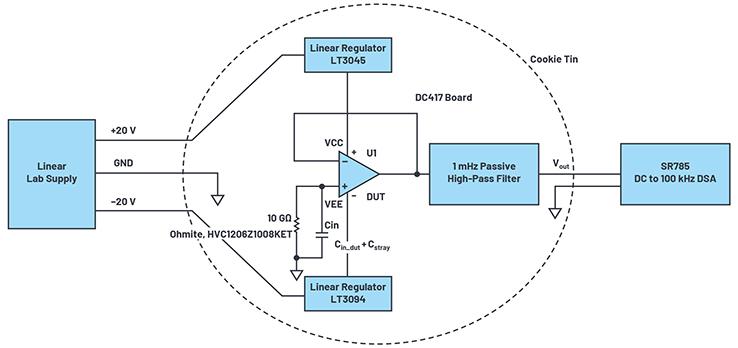 Auf die Messanordnung kommt es an
Abbildung 3. Messanordnung.
Bevor wir darauf eingehen, warum das so ist, wollen wir uns kurz die Messanordnung anschauen. Es braucht eine einfach zu reproduzierende, zuverlässige Messmethode, die auf viele unterschiedliche Bauteiltypen anwendbar ist.
Für die Messungen kann das Verstärker-Evalutionsboard DC417B verwendet werden. Die zur Speisung des Messobjekts (DUT, device under test) verwendete Stromversorgung muss rausch- und driftarm sein. Lineare Stromversorgungen sind Schaltnetzteilen vorzuziehen, um Einflüsse von Schaltrauschen und ähnlichen Artefakten auf die Messung auszuschließen. Das Ausgangsrauschen der Laborstromversorgung lässt sich mithilfe der ultra-rauscharmen Linear-Nachregler LT3045 (positiv) und LT3094 (negativ), die sich durch eine extrem hohe Störunterdrückung (PSRR, power supply rejection ratio) auszeichnen, weiter reduzieren. Bei Verwendung der Linearregler LT3045 und LT3094 kann über einen einzigen Widerstand die benötigte Ausgangsspannung im Bereich von +15 V bis –15 V eingestellt werden. Diese beiden Bausteine sind ideale Nachregler für rauscharme Messungen.
Zur Umsetzung des Stromrauschens in eine Rauschspannung dient ein 10-GΩ-SMT-Widerstand von Ohmite (HVC1206Z1008KET) am nichtinvertierenden Eingang des Messobjekts. Der typische Biasstrom von Verstärkern mit FET-Eingang beträgt etwa 1 pA, was 0.57 fA/√Hz entspricht, sofern die Gleichung
Auf die Messanordnung kommt es an
Abbildung 3. Messanordnung.
Bevor wir darauf eingehen, warum das so ist, wollen wir uns kurz die Messanordnung anschauen. Es braucht eine einfach zu reproduzierende, zuverlässige Messmethode, die auf viele unterschiedliche Bauteiltypen anwendbar ist.
Für die Messungen kann das Verstärker-Evalutionsboard DC417B verwendet werden. Die zur Speisung des Messobjekts (DUT, device under test) verwendete Stromversorgung muss rausch- und driftarm sein. Lineare Stromversorgungen sind Schaltnetzteilen vorzuziehen, um Einflüsse von Schaltrauschen und ähnlichen Artefakten auf die Messung auszuschließen. Das Ausgangsrauschen der Laborstromversorgung lässt sich mithilfe der ultra-rauscharmen Linear-Nachregler LT3045 (positiv) und LT3094 (negativ), die sich durch eine extrem hohe Störunterdrückung (PSRR, power supply rejection ratio) auszeichnen, weiter reduzieren. Bei Verwendung der Linearregler LT3045 und LT3094 kann über einen einzigen Widerstand die benötigte Ausgangsspannung im Bereich von +15 V bis –15 V eingestellt werden. Diese beiden Bausteine sind ideale Nachregler für rauscharme Messungen.
Zur Umsetzung des Stromrauschens in eine Rauschspannung dient ein 10-GΩ-SMT-Widerstand von Ohmite (HVC1206Z1008KET) am nichtinvertierenden Eingang des Messobjekts. Der typische Biasstrom von Verstärkern mit FET-Eingang beträgt etwa 1 pA, was 0.57 fA/√Hz entspricht, sofern die Gleichung
 gilt. Das thermische Rauschen der 10-GΩ-Quellimpedanz beträgt
gilt. Das thermische Rauschen der 10-GΩ-Quellimpedanz beträgt
 Daraus resultiert ein Stromrauschen der Messanordnung von
Daraus resultiert ein Stromrauschen der Messanordnung von
 das bei der Auswertung der Messergebnisse herausgerechnet werden kann. Allerdings sind keine genauen Messungen möglich, wenn das Stromrauschen des Widerstands das Stromrauschen des Messobjekts übersteigt. Deshalb benötigen wir einen Widerstandswert von mindestens 10 GΩ, um das Rauschen des Messobjekts beobachten zu können.
das bei der Auswertung der Messergebnisse herausgerechnet werden kann. Allerdings sind keine genauen Messungen möglich, wenn das Stromrauschen des Widerstands das Stromrauschen des Messobjekts übersteigt. Deshalb benötigen wir einen Widerstandswert von mindestens 10 GΩ, um das Rauschen des Messobjekts beobachten zu können.
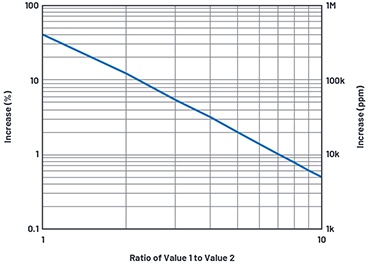 Abbildung 4. RSS-Addition auf der Basis des Verhältnisses zweier Werte.
Bei einem Widerstandswert von 100 MΩ würde das thermische Rauschen der Quellimpedanz etwa 1,28 µV/√Hz (= 12,8 fA/√Hz) betragen, dann könnte man nicht mehr zwischen dem Stromrauschen des Messobjekts und dem des Widerstands unterscheiden. Falls das Rauschen unkorreliert ist, addieren sich die Rauschsignale geometisch (RSS, root sum squared). Abbildung 4 und Tabelle 1 zeigen die RSS-Summen für verschiedene Verhältnisse von zwei Werten und die entsprechende Zunahme des Gesamtrauschens. Bei einem Verhältnis von n:n nimmt das Rauschen um 41% zu, bei n:n/2 um etwa 12%, bei n:n/3 um etwa 5,5% und bei n:n/5 um etwa 2%. Bei Mittelung über hinreichend viele Zyklen könnten wir auf etwa 10% (0,57 fA/√Hz und 1,28 fA/√Hz RSS) kommen.
Tabelle 1. RSS-Addition auf der Basis des Verhältnisses zweier Werte
Abbildung 4. RSS-Addition auf der Basis des Verhältnisses zweier Werte.
Bei einem Widerstandswert von 100 MΩ würde das thermische Rauschen der Quellimpedanz etwa 1,28 µV/√Hz (= 12,8 fA/√Hz) betragen, dann könnte man nicht mehr zwischen dem Stromrauschen des Messobjekts und dem des Widerstands unterscheiden. Falls das Rauschen unkorreliert ist, addieren sich die Rauschsignale geometisch (RSS, root sum squared). Abbildung 4 und Tabelle 1 zeigen die RSS-Summen für verschiedene Verhältnisse von zwei Werten und die entsprechende Zunahme des Gesamtrauschens. Bei einem Verhältnis von n:n nimmt das Rauschen um 41% zu, bei n:n/2 um etwa 12%, bei n:n/3 um etwa 5,5% und bei n:n/5 um etwa 2%. Bei Mittelung über hinreichend viele Zyklen könnten wir auf etwa 10% (0,57 fA/√Hz und 1,28 fA/√Hz RSS) kommen.
Tabelle 1. RSS-Addition auf der Basis des Verhältnisses zweier Werte
Warum sind die Ergebnisse so seltsam?
Abbildung 5 zeigt die mit der beschriebenen Messanordnung ermittelte Rauschspannungsdichte des AD8065, eines 145-MHz-Operationsverstärkers mit FET-Eingang und einer Gleichtakt-Eingangsimpedanz von 2,1 pF. Das thermische Rauschen des 10-GΩ-Widerstands beträgt 12,8 µV/√Hz bis zu der Frequenz, ab der sich die Eingangskapazität und parasitären Kapazitäten der Leiterplatte und Bauteilsockel als Tiefpassfilter bemerkbar machen und das Rauschen mit zunehmender Frequenz immer stärker abfallen lassen. Im Idealfall ergäbe sich ein Abfall mit einer Steilheit von –20 dB/Dekade, doch bei etwa 100 Hz beginnt die Kurve sich abzuflachen und bei etwa 100 kHz verläuft sie nahezu horizontal. Was geht hier vor? Unsere Intuition sagt uns, dass der –20 dB/Dekade-Abfall nur gestoppt werden kann, wenn er durch einen +20 dB/Dekade-Anstieg an anderer Stelle kompensiert wird. Und so ist es auch: Für diesen Kurvenverlauf ist das Stromrauschen "verantwortlich", das bei höheren Frequenzen mit +20 dB/Dekade zunimmt.
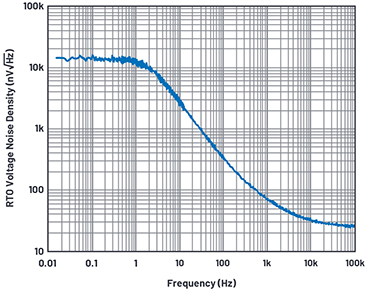 Abbildung 5. Ausgangsbezogene Rauschspannungsdichte.
Das Ausgangsspannungsrauschen kann mithilfe eines Dynamiksignalanalysators SR785 oder eines Oszilloskops mit FFT-Funktion gemessen werden; das Grundrauschen des Messgeräts sollte möglichst unter 7 nV/√Hz liegen. Wenn das Ausgangsrauschen des Messobjekts sich mit zunehmender Frequenz dem Wert 20 nV/√Hz bis 30 nV/√Hz nähert, möchten wir, dass das Analysator-Grundrauschen möglichst wenig zum Gesamtrauschen beiträgt. Bei einem Rauschverhältnis von 1:3 erhöht sich das Gesamtrauschen nur um etwa 5.5%. Das ist ein Wert, mit dem man bei Rauschmessungen leben kann (siehe Abbildung 4).
Die Kunst besteht in der Rückrechnung
Bei der beschriebenen Vorgehensweise werden die beiden wichtigsten Parameter, die zur Darstellung des Stromrauschens über der Frequenz benötigt werden, mit einer einzigen Messung erfasst. Zuerst messen wir die Gesamteingangskapazität, bestehend aus der Eingangskapazität des Messobjekts und den Parasitärkapazitäten. Das ist notwendig, damit wir den Roll-off herausrechnen können. Trotz der Parasitärkapazitäten wurde die gesuchte Information erfasst. Die Eingangskapazität dominiert über den 10-GΩ-Widerstand. Diese Gesamtimpedanz wandelt den Rauschstrom in eine Rauschspannung um. Deshalb ist es wichtig, diese Gesamtkapazität zu kennen. Weiter zeigt dieser Wert, ab welcher Frequenz das Stromrauschen zu dominieren beginnt – nämlich dort, wo die Kurve von dem –20 dB/Dekade-Abfall abzuweichen beginnt.
Schauen wir uns das Beispiel in Abbildung 5 an. Der 3-dB-Roll-off-Punkt liegt bei 2,1 Hz. Daraus errechnet sich eine Gesamtkapazität von
Abbildung 5. Ausgangsbezogene Rauschspannungsdichte.
Das Ausgangsspannungsrauschen kann mithilfe eines Dynamiksignalanalysators SR785 oder eines Oszilloskops mit FFT-Funktion gemessen werden; das Grundrauschen des Messgeräts sollte möglichst unter 7 nV/√Hz liegen. Wenn das Ausgangsrauschen des Messobjekts sich mit zunehmender Frequenz dem Wert 20 nV/√Hz bis 30 nV/√Hz nähert, möchten wir, dass das Analysator-Grundrauschen möglichst wenig zum Gesamtrauschen beiträgt. Bei einem Rauschverhältnis von 1:3 erhöht sich das Gesamtrauschen nur um etwa 5.5%. Das ist ein Wert, mit dem man bei Rauschmessungen leben kann (siehe Abbildung 4).
Die Kunst besteht in der Rückrechnung
Bei der beschriebenen Vorgehensweise werden die beiden wichtigsten Parameter, die zur Darstellung des Stromrauschens über der Frequenz benötigt werden, mit einer einzigen Messung erfasst. Zuerst messen wir die Gesamteingangskapazität, bestehend aus der Eingangskapazität des Messobjekts und den Parasitärkapazitäten. Das ist notwendig, damit wir den Roll-off herausrechnen können. Trotz der Parasitärkapazitäten wurde die gesuchte Information erfasst. Die Eingangskapazität dominiert über den 10-GΩ-Widerstand. Diese Gesamtimpedanz wandelt den Rauschstrom in eine Rauschspannung um. Deshalb ist es wichtig, diese Gesamtkapazität zu kennen. Weiter zeigt dieser Wert, ab welcher Frequenz das Stromrauschen zu dominieren beginnt – nämlich dort, wo die Kurve von dem –20 dB/Dekade-Abfall abzuweichen beginnt.
Schauen wir uns das Beispiel in Abbildung 5 an. Der 3-dB-Roll-off-Punkt liegt bei 2,1 Hz. Daraus errechnet sich eine Gesamtkapazität von
 am Eingang. Aus dem Datenblatt zum Messobjekt entnehmen wir, dass dessen Eingangskapazität nur etwa 2,1 pF beträgt. Das bedeutet, dass die Parasitärkapazitäten zusammen etwa 5,5 pF betragen. Die Gegentakt-Eingangskapazität wird mittels Bootstrapping verringert und spielt daher bei niedrigen Frequenzen keine signifikante Rolle. Abbildung 6 zeigt die Gesamtkapazität aus 10 GΩ parallel 7,6 pF, mit der das Stromrauschen "konfrontiert" ist.
am Eingang. Aus dem Datenblatt zum Messobjekt entnehmen wir, dass dessen Eingangskapazität nur etwa 2,1 pF beträgt. Das bedeutet, dass die Parasitärkapazitäten zusammen etwa 5,5 pF betragen. Die Gegentakt-Eingangskapazität wird mittels Bootstrapping verringert und spielt daher bei niedrigen Frequenzen keine signifikante Rolle. Abbildung 6 zeigt die Gesamtkapazität aus 10 GΩ parallel 7,6 pF, mit der das Stromrauschen "konfrontiert" ist.
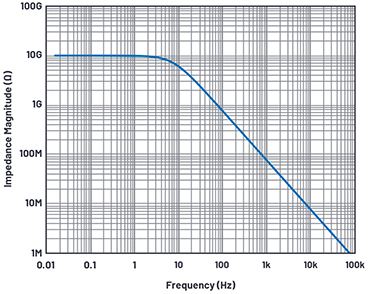 Abbildung 6. Betrag der Gesamtimpedanz der Parallelschaltung aus 10-GΩ-Widerstand und 7,6 pF Gesamtkapazität.
Wenn man die am AD8065 gemessene ausgangsbezogene (RTO, referred to output) Rauschspannung (Abbildung 5) durch die frequenzabhängige Impedanz (Abbildung 6) dividiert, erhält man das äquivalente Stromrauschen des AD8065, kombiniert mit dem Stromrauschen des 10-GΩ-Widerstands gemäß RSS (Abbildung 7).
Abbildung 8 zeigt das eingangsbezogene Stromrauschen des AD8065 nach Herausrechnen des Stromrauschens des 10-GΩ-Widerstands. Unterhalb 10 Hz ist die Kurve stark "zerfleddert", weil wir versucht haben, die 0,5 fA/√Hz bis 0,6 fA/√Hz aus 1,28 fA/√Hz (10% auf der RSS-Skala) herauszufischen und nur 100 Mittelungen ausgeführt wurden. Zwischen 15 mHz und 1,56 Hz liegen bei einer Auflösungsbandbreite von 4 mHz nicht weniger als 400 Spektrallinien – dadurch dauert eine einzige Mittelung 256 Sekunden! Für 100 Mittelungen benötigt man demnach 25.600 Sekunden, das sind etwas mehr als 7 Stunden.
Abbildung 6. Betrag der Gesamtimpedanz der Parallelschaltung aus 10-GΩ-Widerstand und 7,6 pF Gesamtkapazität.
Wenn man die am AD8065 gemessene ausgangsbezogene (RTO, referred to output) Rauschspannung (Abbildung 5) durch die frequenzabhängige Impedanz (Abbildung 6) dividiert, erhält man das äquivalente Stromrauschen des AD8065, kombiniert mit dem Stromrauschen des 10-GΩ-Widerstands gemäß RSS (Abbildung 7).
Abbildung 8 zeigt das eingangsbezogene Stromrauschen des AD8065 nach Herausrechnen des Stromrauschens des 10-GΩ-Widerstands. Unterhalb 10 Hz ist die Kurve stark "zerfleddert", weil wir versucht haben, die 0,5 fA/√Hz bis 0,6 fA/√Hz aus 1,28 fA/√Hz (10% auf der RSS-Skala) herauszufischen und nur 100 Mittelungen ausgeführt wurden. Zwischen 15 mHz und 1,56 Hz liegen bei einer Auflösungsbandbreite von 4 mHz nicht weniger als 400 Spektrallinien – dadurch dauert eine einzige Mittelung 256 Sekunden! Für 100 Mittelungen benötigt man demnach 25.600 Sekunden, das sind etwas mehr als 7 Stunden.
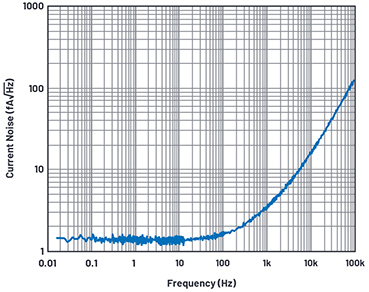 Abbildung 7. RTI-Stromrauschen des AD8065 und eines 10-GΩ-Widerstands.
Warum muss man bis hinab zu 15 mHz messen und dafür so viel Zeit aufwenden? Eine Kapazität von 10 pF ergibt bei einem Widerstand von 10 GΩ ein Tiefpassfilter mit einer Grenzfrequenz von 1,6 Hz. Rauscharme Verstärker mit FET-Eingang haben große Eingangskapazitäten bis zu 20 pF, das ergibt eine –3-dB-Grenzfrequenz von 0,8 Hz. Um den –3-dB-Punkt korrekt messen zu können, müssten wir einen 20-dB-Abfall unterhalb von 0,08 Hz (or 80 mHz) beobachten können.
Eine genauere Analyse des "zerfledderten" Kurvenbereichs unterhalb von 10 Hz ergibt eine Rauschstromdichte von 0,6 fA/√Hz; einen ähnlichen Wert liefert auch die Gleichung
Abbildung 7. RTI-Stromrauschen des AD8065 und eines 10-GΩ-Widerstands.
Warum muss man bis hinab zu 15 mHz messen und dafür so viel Zeit aufwenden? Eine Kapazität von 10 pF ergibt bei einem Widerstand von 10 GΩ ein Tiefpassfilter mit einer Grenzfrequenz von 1,6 Hz. Rauscharme Verstärker mit FET-Eingang haben große Eingangskapazitäten bis zu 20 pF, das ergibt eine –3-dB-Grenzfrequenz von 0,8 Hz. Um den –3-dB-Punkt korrekt messen zu können, müssten wir einen 20-dB-Abfall unterhalb von 0,08 Hz (or 80 mHz) beobachten können.
Eine genauere Analyse des "zerfledderten" Kurvenbereichs unterhalb von 10 Hz ergibt eine Rauschstromdichte von 0,6 fA/√Hz; einen ähnlichen Wert liefert auch die Gleichung
 Diese Gleichung ist demnach bei FETs nicht völlig falsch, sondern zeigt in erster Näherung die niederfrequente Stromrauschcharakteristik des Messobjekts, weil die Messwerte auf dem DC-Eingangsbiasstrom basieren. Bei hohen Frequenzen versagt diese Gleichung jedoch.
Diese Gleichung ist demnach bei FETs nicht völlig falsch, sondern zeigt in erster Näherung die niederfrequente Stromrauschcharakteristik des Messobjekts, weil die Messwerte auf dem DC-Eingangsbiasstrom basieren. Bei hohen Frequenzen versagt diese Gleichung jedoch.
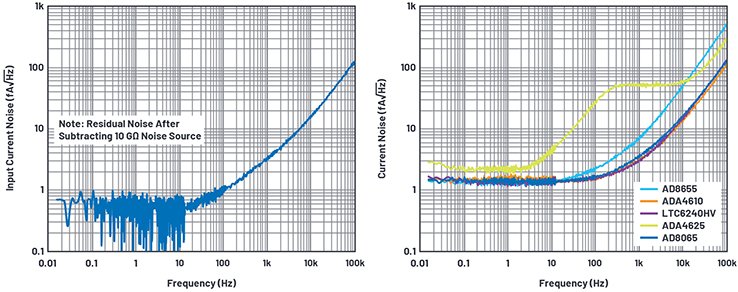 Abbildung 8. RTI-Stromrauschen des AD8605. / Abbildung 9. RTI-Stromrauschen ausgewählter Verstärker von ADI.
Bei höheren Frequenzen dominiert das Stromrauschen des Messobjekts dasjenige des Widerstands signifikant; deshalb kann letzteres vernachlässigt werden. Abbildung 9 zeigt das eingangsbezogene Stromrauschen diverser Verstärker mit FET-Eingang bei 10 GΩ, gemessen mit der Messanordnung von Abbildung 3. Offenbar ist etwa 100 fA/√Hz bei 100 kHz ein typischer Wert, den man bei den meisten Präzisionsverstärkern erwarten darf.
Abbildung 8. RTI-Stromrauschen des AD8605. / Abbildung 9. RTI-Stromrauschen ausgewählter Verstärker von ADI.
Bei höheren Frequenzen dominiert das Stromrauschen des Messobjekts dasjenige des Widerstands signifikant; deshalb kann letzteres vernachlässigt werden. Abbildung 9 zeigt das eingangsbezogene Stromrauschen diverser Verstärker mit FET-Eingang bei 10 GΩ, gemessen mit der Messanordnung von Abbildung 3. Offenbar ist etwa 100 fA/√Hz bei 100 kHz ein typischer Wert, den man bei den meisten Präzisionsverstärkern erwarten darf.
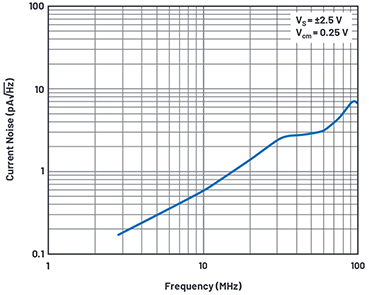 Abbildung 10. Eingangsbezogenes Stromrauschen des LTC6268.
Eine Ausnahme stellen die Typen LTC6268/LTC6269 dar, die bei 100 kHz ein Stromrauschen von nur 5,6 fA/√Hz aufweisen. Diese Verstärker eignen sich hervorragend für schnelle Transimpedanz- (TIA) Anwendungen, die große Bandbreite, geringe Eingangskapazität und Biasströme im Femtoampere-Bereich erfordern.
Ist das alles, was es zum Stromrauschen von Verstärkern mit FET-Eingang anzumerken gibt?
Nein. Insgesamt gibt es vier Rauschquellen, die signifikant zum Gesamt-Eingangsstromrauschen in Anwendungen mit hoher Quellimpedanz beitragen. Bisher wurden nur zwei davon behandelt. Abbildung 11 zeigt ein vereinfachtes Modell des Operationsverstärkers aus MT-050, das als gutes Beispiel für die Rauschquellen eines Operationsverstärkers dienen kann.
Abbildung 10. Eingangsbezogenes Stromrauschen des LTC6268.
Eine Ausnahme stellen die Typen LTC6268/LTC6269 dar, die bei 100 kHz ein Stromrauschen von nur 5,6 fA/√Hz aufweisen. Diese Verstärker eignen sich hervorragend für schnelle Transimpedanz- (TIA) Anwendungen, die große Bandbreite, geringe Eingangskapazität und Biasströme im Femtoampere-Bereich erfordern.
Ist das alles, was es zum Stromrauschen von Verstärkern mit FET-Eingang anzumerken gibt?
Nein. Insgesamt gibt es vier Rauschquellen, die signifikant zum Gesamt-Eingangsstromrauschen in Anwendungen mit hoher Quellimpedanz beitragen. Bisher wurden nur zwei davon behandelt. Abbildung 11 zeigt ein vereinfachtes Modell des Operationsverstärkers aus MT-050, das als gutes Beispiel für die Rauschquellen eines Operationsverstärkers dienen kann.
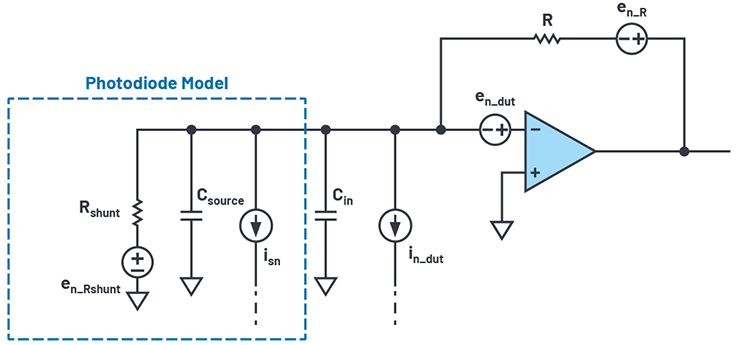 Abbildung 11. Vereinfachtes Modell eines TIA-Verstärkers einschließlich der wichtigsten Rauschquellen.
Stromrauschen aus dem FET-Eingang (in_dut)
Die Stromrauschkurve hängt von der Topologie der Eingangsstufe des Verstärkers ab. Im Allgemeinen ist die Kurve bei niedrigen Frequenzen flach und steigt mit zunehmender Frequenz an. Siehe Abbildung 8. Ab der Grenzfrequenz des Verstärkers sinkt die Verstärkung, und die Rauschkurve geht in einen –20-dB/Dekade-Verlauf über.
Stromrauschen aus dem Widerstand (in_R)
Diese Rauschkomponente kann man berechnen, indem man das thermischen Spannungsrauschen des Widerstands, en_R, durch die Impedanz des Widerstands R dividiert. 1 MΩ trägt etwa 128 fA/√Hz bei, 10 GΩ etwa 1,28 fA/√Hz.
Abbildung 11. Vereinfachtes Modell eines TIA-Verstärkers einschließlich der wichtigsten Rauschquellen.
Stromrauschen aus dem FET-Eingang (in_dut)
Die Stromrauschkurve hängt von der Topologie der Eingangsstufe des Verstärkers ab. Im Allgemeinen ist die Kurve bei niedrigen Frequenzen flach und steigt mit zunehmender Frequenz an. Siehe Abbildung 8. Ab der Grenzfrequenz des Verstärkers sinkt die Verstärkung, und die Rauschkurve geht in einen –20-dB/Dekade-Verlauf über.
Stromrauschen aus dem Widerstand (in_R)
Diese Rauschkomponente kann man berechnen, indem man das thermischen Spannungsrauschen des Widerstands, en_R, durch die Impedanz des Widerstands R dividiert. 1 MΩ trägt etwa 128 fA/√Hz bei, 10 GΩ etwa 1,28 fA/√Hz.
 Das thermische Spannungsrauschen des Widerstands zeigt bis einer gewissen Frequenz ein völlig flaches Verhalten und geht oberhalb dieser Frequenz allmählich in einen –20-dB/Dekade-Abfall über. Siehe Abbildung 5.
Stromrauschen aus dem Sensor (in_source)
Der Sensor trägt seinen Anteil am Stromrauschen bei, damit müssen wir leben. Der Frequenzverlauf dieser Rauschkomponente kann höchst unterschiedlich sein. Eine Photodiode, beispielsweise, produziert Schrotrauschen, Isn, aus dem Photostrom, IP, und dem Dunkelstrom, ID, sowie Johnson-Rauschen, Ijn, aus dem Shunt-Widerstand.1
Das thermische Spannungsrauschen des Widerstands zeigt bis einer gewissen Frequenz ein völlig flaches Verhalten und geht oberhalb dieser Frequenz allmählich in einen –20-dB/Dekade-Abfall über. Siehe Abbildung 5.
Stromrauschen aus dem Sensor (in_source)
Der Sensor trägt seinen Anteil am Stromrauschen bei, damit müssen wir leben. Der Frequenzverlauf dieser Rauschkomponente kann höchst unterschiedlich sein. Eine Photodiode, beispielsweise, produziert Schrotrauschen, Isn, aus dem Photostrom, IP, und dem Dunkelstrom, ID, sowie Johnson-Rauschen, Ijn, aus dem Shunt-Widerstand.1
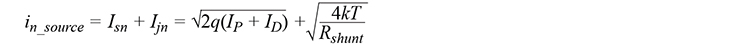 Stromrauschen aus dem Spannungsrauschen des Verstärkers
Das Stromrauschen aus dem Spannungsrauschen des Verstärkers wird als enC-Rauschen bezeichnet und in The Art of Electronics von Horowitz und Hill sehr gut erklärt.2 Ähnlich wie das Spannungsrauschen des Widerstands durch den Widerstand selbst in ein Stromrauschen umgewandelt wird, wird das Spannungsrauschen des Verstärkers, en_dut , durch die Gesamt-Eingangskapazität – die sich aus der Sensorkapazität, den Parasitärkapazitäten der Leiterplatte und der Eingangskapazität des Verstärker zusammensetzt – in Stromrauschen umgewandelt.
Stromrauschen aus dem Spannungsrauschen des Verstärkers
Das Stromrauschen aus dem Spannungsrauschen des Verstärkers wird als enC-Rauschen bezeichnet und in The Art of Electronics von Horowitz und Hill sehr gut erklärt.2 Ähnlich wie das Spannungsrauschen des Widerstands durch den Widerstand selbst in ein Stromrauschen umgewandelt wird, wird das Spannungsrauschen des Verstärkers, en_dut , durch die Gesamt-Eingangskapazität – die sich aus der Sensorkapazität, den Parasitärkapazitäten der Leiterplatte und der Eingangskapazität des Verstärker zusammensetzt – in Stromrauschen umgewandelt.
 Zunächst erhalten wir:
Zunächst erhalten wir:
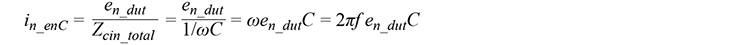 Diese Gleichung lehrt uns drei Dinge. Erstens: Das Stromrauschen wird mit zunehmender Frequenz stärker – noch eine weitere Komponente des Stromrauschens, die diese Eigenschaft aufweist. Zweitens: Je größer das Eingangsspannungsrauschen des Verstärkers ist, desto größer auch das Stromrauschen. Drittens: Je größer die Gesamt-Eingangskapazität ist, desto größer ist auch das Stromrauschen. Das führt zu einer Gütezahl ("figure of merit") enC, die in einer gegeben Anwendung sowohl das Spannungsrauschen des Verstärkers als auch die Gesamt-Eingangskapazität berücksichtigt.
Abbildung 12 zeigt die Stromrauschkurve für TIA-Anwendungen, die das Stromrauschen des Messobjekts vernachlässigt. Der flache Teil der Kurve beschreibt im Wesentlichen das Widerstandsrauschen.
Diese Gleichung lehrt uns drei Dinge. Erstens: Das Stromrauschen wird mit zunehmender Frequenz stärker – noch eine weitere Komponente des Stromrauschens, die diese Eigenschaft aufweist. Zweitens: Je größer das Eingangsspannungsrauschen des Verstärkers ist, desto größer auch das Stromrauschen. Drittens: Je größer die Gesamt-Eingangskapazität ist, desto größer ist auch das Stromrauschen. Das führt zu einer Gütezahl ("figure of merit") enC, die in einer gegeben Anwendung sowohl das Spannungsrauschen des Verstärkers als auch die Gesamt-Eingangskapazität berücksichtigt.
Abbildung 12 zeigt die Stromrauschkurve für TIA-Anwendungen, die das Stromrauschen des Messobjekts vernachlässigt. Der flache Teil der Kurve beschreibt im Wesentlichen das Widerstandsrauschen.
 Das kapazitätsbedingte Stromrauschen berechnet sich nach folgender Gleichung:
Das kapazitätsbedingte Stromrauschen berechnet sich nach folgender Gleichung:
 Es steigt um 20 dB/Dekade an. Aus den beiden Gleichungen lässt sich der Schnittpunkt berechnen:
Es steigt um 20 dB/Dekade an. Aus den beiden Gleichungen lässt sich der Schnittpunkt berechnen:
 Je nach Cin kann das enC-Rauschen größer oder kleiner als das Stromrauschen des Messobjekts sein. Bei invertierenden Schaltungen, beispielsweise in TIA-Anwendungen, wird Cdm nicht "gebootstrapped"; es gilt
Je nach Cin kann das enC-Rauschen größer oder kleiner als das Stromrauschen des Messobjekts sein. Bei invertierenden Schaltungen, beispielsweise in TIA-Anwendungen, wird Cdm nicht "gebootstrapped"; es gilt
 Für den LTC6244, beispielsweise, gelten bei 100 kHz die folgenden Werte: Ccm = 2,1 pF, Cdm = 3,5 pF und en = 8 nV/√Hz. Daraus berechnet sich ein enC-Stromrauschen von
Für den LTC6244, beispielsweise, gelten bei 100 kHz die folgenden Werte: Ccm = 2,1 pF, Cdm = 3,5 pF und en = 8 nV/√Hz. Daraus berechnet sich ein enC-Stromrauschen von
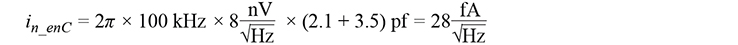 Dieser Wert ist wesentlich kleiner als das Stromrauschen des Messobjekts von 80 fA/vHz
Dieser Wert ist wesentlich kleiner als das Stromrauschen des Messobjekts von 80 fA/vHz
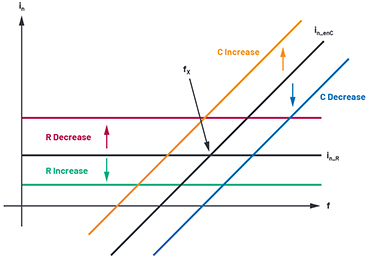 Abbildung 12. enC-Rauschen über der Frequenz.
Wenn jedoch eine Photodiode angeschlossen ist, ist eine zusätzliche Kapazität Csource oder Cpd zur Gleichung hinzu zu addieren, und das Stromrauschen muss neu berechnet werden. Schon bei einer kleinen Cpd-Kapazität von nur 16 pF steigt das enC-Stromrauschen auf ähnliche Werte wie das Stromrauschen des Messobjekts an. Langsame, großflächige Photodioden haben meistens Kapazitäten in der Größenordnung von 100 pF bis 1 nF, kleinflächige High-Speed-Typen dagegen Werte von etwa 1 pF bis 10 pF.
Zusammenfassung
Das Phänomen, dass sowohl bei Verstärkern mit CMOS- als auch solchen mit JFET-Eingang das Stromrauschen mit ansteigender Frequenz zunimmt, ist IC-Designern und erfahrenen Schaltungsentwicklern bekannt. Es war vielen Ingenieuren jedoch nicht zugänglich, weil es entweder zu wenige Fachartikel auf diesem Gebiet gab oder weil die Informationen der Halbleiterhersteller unvollständig waren. Ziel dieses Artikel ist es, zu einem besseren Verständnis des Stromrauschens bei höheren Frequenzen beizutragen und eine Technik für reproduzierbare Rauschmessungen am Operationsverstärker der Wahl zu beschreiben.
Weiterführende Informationen
Die Auswahl des für eine gegebene Anwendung optimalen Operationsverstärkers ist keine einfache Aufgabe. Je nach Anwendung muss man Kompromisse zwischen Rauschen, Bandbreite, Verstärkung und Genauigkeit eingehen. Die untenstehenden Literaturhinweise 1, 2, 3, 4, 5, 6 und 7 sowie zahlreiche Datenblätter informieren ausführlich darüber, was dabei zu beachten ist.
Literaturhinweise
Abbildung 12. enC-Rauschen über der Frequenz.
Wenn jedoch eine Photodiode angeschlossen ist, ist eine zusätzliche Kapazität Csource oder Cpd zur Gleichung hinzu zu addieren, und das Stromrauschen muss neu berechnet werden. Schon bei einer kleinen Cpd-Kapazität von nur 16 pF steigt das enC-Stromrauschen auf ähnliche Werte wie das Stromrauschen des Messobjekts an. Langsame, großflächige Photodioden haben meistens Kapazitäten in der Größenordnung von 100 pF bis 1 nF, kleinflächige High-Speed-Typen dagegen Werte von etwa 1 pF bis 10 pF.
Zusammenfassung
Das Phänomen, dass sowohl bei Verstärkern mit CMOS- als auch solchen mit JFET-Eingang das Stromrauschen mit ansteigender Frequenz zunimmt, ist IC-Designern und erfahrenen Schaltungsentwicklern bekannt. Es war vielen Ingenieuren jedoch nicht zugänglich, weil es entweder zu wenige Fachartikel auf diesem Gebiet gab oder weil die Informationen der Halbleiterhersteller unvollständig waren. Ziel dieses Artikel ist es, zu einem besseren Verständnis des Stromrauschens bei höheren Frequenzen beizutragen und eine Technik für reproduzierbare Rauschmessungen am Operationsverstärker der Wahl zu beschreiben.
Weiterführende Informationen
Die Auswahl des für eine gegebene Anwendung optimalen Operationsverstärkers ist keine einfache Aufgabe. Je nach Anwendung muss man Kompromisse zwischen Rauschen, Bandbreite, Verstärkung und Genauigkeit eingehen. Die untenstehenden Literaturhinweise 1, 2, 3, 4, 5, 6 und 7 sowie zahlreiche Datenblätter informieren ausführlich darüber, was dabei zu beachten ist.
Literaturhinweise
 Abbildung 13. Messanordnung..
Bei einem typischen IC mit einem einzigen Verstärker befindet sich Pin3 (Vin+) unmittelbar neben Pin4 (V–). Falls kein Guard-Ring vorhanden ist, spielt das Leiterplattenlayout eine entscheidende Rolle. Bei Betriebsspannungsänderungen änderte sich auch der Gleichspannungsanteil der Ausgangsspannung signifikant. Der 10-GΩ-SMD-Widerstand war ursprünglich parallel zu V– (R10 in Abbildung 13) eingelötet, und der Leckstrom durch die Lotpaste war inakzeptabel. Deshalb wurde der 10-GΩ-SMD-Widerstand an anderer Stelle angebracht (R8), woraufhin der Leckstrom verschwand. Das Datenblatt zum ADA4530-1 (Verstärker der Elektrometerklasse mit 20 fA bei 85°C) beschreibt alle Vorkehrungen hinsichtlich Auswahl der Lotpaste, Verschmutzung, Feuchtigkeit und anderer Einflussgrößen, die bei Hochimpedanzmessungen getroffen werden müssen. Es lohnt sich, das Datenblatt und den User Guide UG-865 sowie die Circuit Note CN-0407 zu lesen.
Nicht-schallisolierte Bauteile mit hoher Eingangsimpedanz können triboelektrischen, piezoelektrischen und mikrophonischen Effekten unterliegen. Irgendwann einmal habe ich unbeabsichtigt meinen Schlüsselbund fallen lassen und bemerkte im Messdiagramm einen Spike im hörbaren Frequenzbereich (insbesondere 1 kHz und darüber). Ich hätte nicht gedacht, dass Messungen an einer hochimpedanten FET-Eingangsstufe mit 10 GΩ Eingangswiderstand derart schallempfindlich sein könnten. Um mich zu vergewissern, pfiff ich – und siehe da, ich bekam einen Spike zwischen 1 kHz und 2 kHz zu sehen. Selbst bei Messdatenmittelung über zahlreiche Zyklen genügt ein kurzes Pfeifen, um im CRT-Diagramm des SR785 einen Spike hervorzurufen. Die in CN-0407 erwähnten, hermetisch dichten Glaswiderstände wären im Hinblick auf tribo-/piezoelektrische Effekte eine bessere Wahl.
Abbildung 13. Messanordnung..
Bei einem typischen IC mit einem einzigen Verstärker befindet sich Pin3 (Vin+) unmittelbar neben Pin4 (V–). Falls kein Guard-Ring vorhanden ist, spielt das Leiterplattenlayout eine entscheidende Rolle. Bei Betriebsspannungsänderungen änderte sich auch der Gleichspannungsanteil der Ausgangsspannung signifikant. Der 10-GΩ-SMD-Widerstand war ursprünglich parallel zu V– (R10 in Abbildung 13) eingelötet, und der Leckstrom durch die Lotpaste war inakzeptabel. Deshalb wurde der 10-GΩ-SMD-Widerstand an anderer Stelle angebracht (R8), woraufhin der Leckstrom verschwand. Das Datenblatt zum ADA4530-1 (Verstärker der Elektrometerklasse mit 20 fA bei 85°C) beschreibt alle Vorkehrungen hinsichtlich Auswahl der Lotpaste, Verschmutzung, Feuchtigkeit und anderer Einflussgrößen, die bei Hochimpedanzmessungen getroffen werden müssen. Es lohnt sich, das Datenblatt und den User Guide UG-865 sowie die Circuit Note CN-0407 zu lesen.
Nicht-schallisolierte Bauteile mit hoher Eingangsimpedanz können triboelektrischen, piezoelektrischen und mikrophonischen Effekten unterliegen. Irgendwann einmal habe ich unbeabsichtigt meinen Schlüsselbund fallen lassen und bemerkte im Messdiagramm einen Spike im hörbaren Frequenzbereich (insbesondere 1 kHz und darüber). Ich hätte nicht gedacht, dass Messungen an einer hochimpedanten FET-Eingangsstufe mit 10 GΩ Eingangswiderstand derart schallempfindlich sein könnten. Um mich zu vergewissern, pfiff ich – und siehe da, ich bekam einen Spike zwischen 1 kHz und 2 kHz zu sehen. Selbst bei Messdatenmittelung über zahlreiche Zyklen genügt ein kurzes Pfeifen, um im CRT-Diagramm des SR785 einen Spike hervorzurufen. Die in CN-0407 erwähnten, hermetisch dichten Glaswiderstände wären im Hinblick auf tribo-/piezoelektrische Effekte eine bessere Wahl.
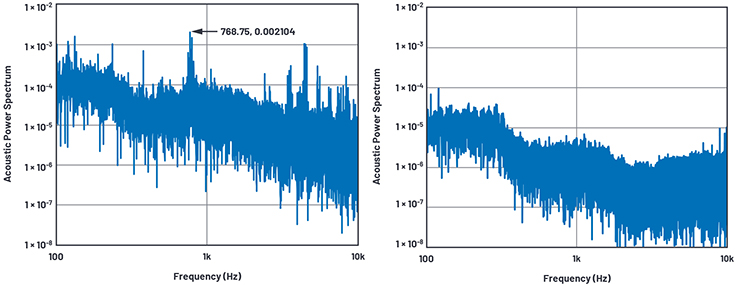 Abbildung 14. Akustische Geräusche im Labor. / Abbildung 15. Akustische Geräusche in der Telefonkabine.
Um der Sache auf den Grund zu gehen, habe ich die Geräusche im Labor mithilfe eines Laptop-Mikrofons aufgenommen, die Messdaten mithilfe von MATLAB® analysiert und herausgefunden, dass die Rauschmessungen mit den Umgebungsgeräuschen korreliert waren. Ein signifikanter, geräuschbedingter Spike trat bei 768 Hz und weiteren Frequenzen auf (siehe Abbildung 14). Verantwortlich dafür war ein großer Netzspannungskabelschacht in ein paar Metern Entfernung von meinem Labortisch. Um sicherzugehen, nicht auch noch das Betriebsgeräusch meines Laptops zu erfassen, ging ich für die Messungen in eine der Telefonkabinen – das sind die ruhigsten Plätze in meiner Arbeitsumgebung. Bei 768 Hz war daraufhin kein Spike mehr zu erkennen, und die Spikes bei anderen Frequenzen waren um mindestens den Faktor 100 kleiner.
Abbildung 14. Akustische Geräusche im Labor. / Abbildung 15. Akustische Geräusche in der Telefonkabine.
Um der Sache auf den Grund zu gehen, habe ich die Geräusche im Labor mithilfe eines Laptop-Mikrofons aufgenommen, die Messdaten mithilfe von MATLAB® analysiert und herausgefunden, dass die Rauschmessungen mit den Umgebungsgeräuschen korreliert waren. Ein signifikanter, geräuschbedingter Spike trat bei 768 Hz und weiteren Frequenzen auf (siehe Abbildung 14). Verantwortlich dafür war ein großer Netzspannungskabelschacht in ein paar Metern Entfernung von meinem Labortisch. Um sicherzugehen, nicht auch noch das Betriebsgeräusch meines Laptops zu erfassen, ging ich für die Messungen in eine der Telefonkabinen – das sind die ruhigsten Plätze in meiner Arbeitsumgebung. Bei 768 Hz war daraufhin kein Spike mehr zu erkennen, und die Spikes bei anderen Frequenzen waren um mindestens den Faktor 100 kleiner.
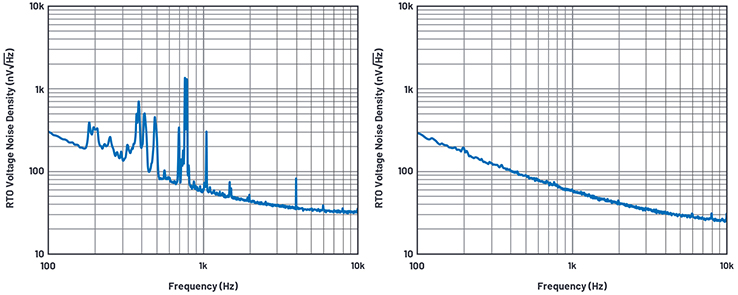 Abbildung 16. Ausgangsbezogene Spannungsrauschdichte ohne akustische Abschirmung. / Abbildung 17. Ausgangsbezogene Spannungsrauschdichte mit akustischer Abschirmung.
Zur Dämpfung der akustischen Geräusche verwendete ich daraufhin eine Temptronix-Box. Die Box scheint temperaturgedämmt zu sein, eine signifikante Luftbewegung findet darin nicht statt. Darauf kam es mir aber nicht an. Es ging mir nur darum, die Messanordnung vor Schall zu schützen – und das tat die Box. Siehe Abbildungen 16 und 17.
Fehlerquellen, an die man vielleicht nicht denkt
Abbildung 16. Ausgangsbezogene Spannungsrauschdichte ohne akustische Abschirmung. / Abbildung 17. Ausgangsbezogene Spannungsrauschdichte mit akustischer Abschirmung.
Zur Dämpfung der akustischen Geräusche verwendete ich daraufhin eine Temptronix-Box. Die Box scheint temperaturgedämmt zu sein, eine signifikante Luftbewegung findet darin nicht statt. Darauf kam es mir aber nicht an. Es ging mir nur darum, die Messanordnung vor Schall zu schützen – und das tat die Box. Siehe Abbildungen 16 und 17.
Fehlerquellen, an die man vielleicht nicht denkt
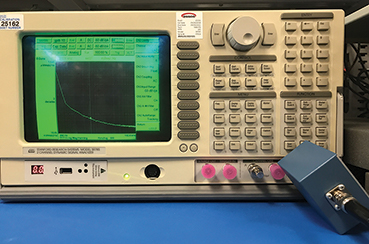 Abbildung 18. Externes Hochpassfilter, zur Minimierung der Störsignale aus dem Analysatorbildschirm gedreht.
Verstärker mit FET-Eingang haben Eingangsströme in der Größenordnung von pA. Bei einem Eingangswiderstand von 10 GΩ produziert ein Eingangsstrom von 10 pA am Verstärkerausgang eine Offsetspannung von 100 mV. Der Eingang des SR785 bietet die Wahl zwischen DC- und AC-Kopplung. In Stellung AC wird dieser Offset ausgeblendet, und man kann das Ausgangsrauschen im Messbereich höchster Empfindlichkeit (–50 dBV-Spitze bzw. 3,2 mV-Spitze) messen. Durch die AC-Kopplung wird jedoch der Frequenzbereich auf eine untere Grenzfrequenz von 1 Hz beschnitten; dadurch ist es schwierig, den flachen 12,8-µV/√Hz-Bereich zu analysieren und den –3 dB-Punkt zu messen.
Deshalb muss man mit DC-Kopplung arbeiten, mit der Folge, dass der empfindlichste Messbereich des Analysators nicht genutzt werden kann. Dieses Problem wurde gelöst, indem dem Eingang des SR785 ein Hochpassfilter mit 1 mHz Grenzfrequenz – bestehend aus zwei polarisierten, in Serie geschalteten 270-µF-Kondensatoren (Gesamtkapazität 135 µF) und einem 1-MΩ-Widerstand – vorgeschaltet wurde. Der Bildschirm des SR785 produziert ein Magnetfeld mit Frequenzen im Bereich von 20 kHz und Oberwellen, das in den Kondensatoren des externen Hochpassfilters Störsignale hervorrufen kann. Diese lassen sich durch Drehen des Filters (blaue Box) minimieren (siehe Abbildung 18).
Über den Autor: Kaung Win begann seine Laufbahn bei Analog Devices im Jahr 2013 als Produkterprobungsingenieur für die Linear Products and Solutions Group. Im Jahr 2019 wechselte er auf eine Stelle als Anwendungsingenieur. Er hat einen Bachelor-Abschluss in Elektro- und Computertechnik vom Worcester Polytechnic Institute und einen Master-Abschluss in Elektrotechnik von der Universität Santa Clara. Sein Spezialgebiet sind Lösungen für die Verstärker-Signalkette. Kaung ist unter kaung.win@analog.com. zu erreichen. / Copyright: © Analog Devices Inc.
Abbildung 18. Externes Hochpassfilter, zur Minimierung der Störsignale aus dem Analysatorbildschirm gedreht.
Verstärker mit FET-Eingang haben Eingangsströme in der Größenordnung von pA. Bei einem Eingangswiderstand von 10 GΩ produziert ein Eingangsstrom von 10 pA am Verstärkerausgang eine Offsetspannung von 100 mV. Der Eingang des SR785 bietet die Wahl zwischen DC- und AC-Kopplung. In Stellung AC wird dieser Offset ausgeblendet, und man kann das Ausgangsrauschen im Messbereich höchster Empfindlichkeit (–50 dBV-Spitze bzw. 3,2 mV-Spitze) messen. Durch die AC-Kopplung wird jedoch der Frequenzbereich auf eine untere Grenzfrequenz von 1 Hz beschnitten; dadurch ist es schwierig, den flachen 12,8-µV/√Hz-Bereich zu analysieren und den –3 dB-Punkt zu messen.
Deshalb muss man mit DC-Kopplung arbeiten, mit der Folge, dass der empfindlichste Messbereich des Analysators nicht genutzt werden kann. Dieses Problem wurde gelöst, indem dem Eingang des SR785 ein Hochpassfilter mit 1 mHz Grenzfrequenz – bestehend aus zwei polarisierten, in Serie geschalteten 270-µF-Kondensatoren (Gesamtkapazität 135 µF) und einem 1-MΩ-Widerstand – vorgeschaltet wurde. Der Bildschirm des SR785 produziert ein Magnetfeld mit Frequenzen im Bereich von 20 kHz und Oberwellen, das in den Kondensatoren des externen Hochpassfilters Störsignale hervorrufen kann. Diese lassen sich durch Drehen des Filters (blaue Box) minimieren (siehe Abbildung 18).
Über den Autor: Kaung Win begann seine Laufbahn bei Analog Devices im Jahr 2013 als Produkterprobungsingenieur für die Linear Products and Solutions Group. Im Jahr 2019 wechselte er auf eine Stelle als Anwendungsingenieur. Er hat einen Bachelor-Abschluss in Elektro- und Computertechnik vom Worcester Polytechnic Institute und einen Master-Abschluss in Elektrotechnik von der Universität Santa Clara. Sein Spezialgebiet sind Lösungen für die Verstärker-Signalkette. Kaung ist unter kaung.win@analog.com. zu erreichen. / Copyright: © Analog Devices Inc.
 Diese ist als Schrotrauschen-Gleichung bekannt. Seit jeher spezifiziert ADI die Rauschzahlen seiner meisten Produkte auf diese Weise. Doch gilt dieser berechnete Wert bei allen Verstärkern für Frequenzen bis 1 kHz?
Diese ist als Schrotrauschen-Gleichung bekannt. Seit jeher spezifiziert ADI die Rauschzahlen seiner meisten Produkte auf diese Weise. Doch gilt dieser berechnete Wert bei allen Verstärkern für Frequenzen bis 1 kHz?
 Abbildung 1. Stromrauschen des bipolaren Verstärkers AD8099. / Abbildung 2. Stromrauschen des Verstärkers AD8065 mit FET-Eingang.
In den letzten Jahren interessierte man sich vermehrt für die Frequenzabhängigkeit des Stromrauschens von Verstärkern. Einige Kunden – wie auch Hersteller – gehen davon aus, dass das Stromrauschen von Verstärkern mit FET-Eingang einen ähnlichen Frequenzverlauf aufweist wie das von Verstärkern mit bipolarer Eingangsstufe, das sich z.B. aus einer Flickerrauschkomponente (1/f) und einer flach verlaufenden Breitbandkomponente zusammensetzt (Abbildung 1). Das ist bei Verstärkern mit FET-Eingang jedoch nicht der Fall. Wie aus Abbildung 2 ersichtlich ist, weisen FETs eine bizarr anmutende Rauschcharakteristik auf, über die wenig bekannt ist und die in vielen Simulationsmodellen nicht korrekt abgebildet wird.
Abbildung 1. Stromrauschen des bipolaren Verstärkers AD8099. / Abbildung 2. Stromrauschen des Verstärkers AD8065 mit FET-Eingang.
In den letzten Jahren interessierte man sich vermehrt für die Frequenzabhängigkeit des Stromrauschens von Verstärkern. Einige Kunden – wie auch Hersteller – gehen davon aus, dass das Stromrauschen von Verstärkern mit FET-Eingang einen ähnlichen Frequenzverlauf aufweist wie das von Verstärkern mit bipolarer Eingangsstufe, das sich z.B. aus einer Flickerrauschkomponente (1/f) und einer flach verlaufenden Breitbandkomponente zusammensetzt (Abbildung 1). Das ist bei Verstärkern mit FET-Eingang jedoch nicht der Fall. Wie aus Abbildung 2 ersichtlich ist, weisen FETs eine bizarr anmutende Rauschcharakteristik auf, über die wenig bekannt ist und die in vielen Simulationsmodellen nicht korrekt abgebildet wird.
 Auf die Messanordnung kommt es an
Abbildung 3. Messanordnung.
Bevor wir darauf eingehen, warum das so ist, wollen wir uns kurz die Messanordnung anschauen. Es braucht eine einfach zu reproduzierende, zuverlässige Messmethode, die auf viele unterschiedliche Bauteiltypen anwendbar ist.
Für die Messungen kann das Verstärker-Evalutionsboard DC417B verwendet werden. Die zur Speisung des Messobjekts (DUT, device under test) verwendete Stromversorgung muss rausch- und driftarm sein. Lineare Stromversorgungen sind Schaltnetzteilen vorzuziehen, um Einflüsse von Schaltrauschen und ähnlichen Artefakten auf die Messung auszuschließen. Das Ausgangsrauschen der Laborstromversorgung lässt sich mithilfe der ultra-rauscharmen Linear-Nachregler LT3045 (positiv) und LT3094 (negativ), die sich durch eine extrem hohe Störunterdrückung (PSRR, power supply rejection ratio) auszeichnen, weiter reduzieren. Bei Verwendung der Linearregler LT3045 und LT3094 kann über einen einzigen Widerstand die benötigte Ausgangsspannung im Bereich von +15 V bis –15 V eingestellt werden. Diese beiden Bausteine sind ideale Nachregler für rauscharme Messungen.
Zur Umsetzung des Stromrauschens in eine Rauschspannung dient ein 10-GΩ-SMT-Widerstand von Ohmite (HVC1206Z1008KET) am nichtinvertierenden Eingang des Messobjekts. Der typische Biasstrom von Verstärkern mit FET-Eingang beträgt etwa 1 pA, was 0.57 fA/√Hz entspricht, sofern die Gleichung
Auf die Messanordnung kommt es an
Abbildung 3. Messanordnung.
Bevor wir darauf eingehen, warum das so ist, wollen wir uns kurz die Messanordnung anschauen. Es braucht eine einfach zu reproduzierende, zuverlässige Messmethode, die auf viele unterschiedliche Bauteiltypen anwendbar ist.
Für die Messungen kann das Verstärker-Evalutionsboard DC417B verwendet werden. Die zur Speisung des Messobjekts (DUT, device under test) verwendete Stromversorgung muss rausch- und driftarm sein. Lineare Stromversorgungen sind Schaltnetzteilen vorzuziehen, um Einflüsse von Schaltrauschen und ähnlichen Artefakten auf die Messung auszuschließen. Das Ausgangsrauschen der Laborstromversorgung lässt sich mithilfe der ultra-rauscharmen Linear-Nachregler LT3045 (positiv) und LT3094 (negativ), die sich durch eine extrem hohe Störunterdrückung (PSRR, power supply rejection ratio) auszeichnen, weiter reduzieren. Bei Verwendung der Linearregler LT3045 und LT3094 kann über einen einzigen Widerstand die benötigte Ausgangsspannung im Bereich von +15 V bis –15 V eingestellt werden. Diese beiden Bausteine sind ideale Nachregler für rauscharme Messungen.
Zur Umsetzung des Stromrauschens in eine Rauschspannung dient ein 10-GΩ-SMT-Widerstand von Ohmite (HVC1206Z1008KET) am nichtinvertierenden Eingang des Messobjekts. Der typische Biasstrom von Verstärkern mit FET-Eingang beträgt etwa 1 pA, was 0.57 fA/√Hz entspricht, sofern die Gleichung
 gilt. Das thermische Rauschen der 10-GΩ-Quellimpedanz beträgt
gilt. Das thermische Rauschen der 10-GΩ-Quellimpedanz beträgt
 Daraus resultiert ein Stromrauschen der Messanordnung von
Daraus resultiert ein Stromrauschen der Messanordnung von
 das bei der Auswertung der Messergebnisse herausgerechnet werden kann. Allerdings sind keine genauen Messungen möglich, wenn das Stromrauschen des Widerstands das Stromrauschen des Messobjekts übersteigt. Deshalb benötigen wir einen Widerstandswert von mindestens 10 GΩ, um das Rauschen des Messobjekts beobachten zu können.
das bei der Auswertung der Messergebnisse herausgerechnet werden kann. Allerdings sind keine genauen Messungen möglich, wenn das Stromrauschen des Widerstands das Stromrauschen des Messobjekts übersteigt. Deshalb benötigen wir einen Widerstandswert von mindestens 10 GΩ, um das Rauschen des Messobjekts beobachten zu können.
 Abbildung 4. RSS-Addition auf der Basis des Verhältnisses zweier Werte.
Bei einem Widerstandswert von 100 MΩ würde das thermische Rauschen der Quellimpedanz etwa 1,28 µV/√Hz (= 12,8 fA/√Hz) betragen, dann könnte man nicht mehr zwischen dem Stromrauschen des Messobjekts und dem des Widerstands unterscheiden. Falls das Rauschen unkorreliert ist, addieren sich die Rauschsignale geometisch (RSS, root sum squared). Abbildung 4 und Tabelle 1 zeigen die RSS-Summen für verschiedene Verhältnisse von zwei Werten und die entsprechende Zunahme des Gesamtrauschens. Bei einem Verhältnis von n:n nimmt das Rauschen um 41% zu, bei n:n/2 um etwa 12%, bei n:n/3 um etwa 5,5% und bei n:n/5 um etwa 2%. Bei Mittelung über hinreichend viele Zyklen könnten wir auf etwa 10% (0,57 fA/√Hz und 1,28 fA/√Hz RSS) kommen.
Tabelle 1. RSS-Addition auf der Basis des Verhältnisses zweier Werte
Abbildung 4. RSS-Addition auf der Basis des Verhältnisses zweier Werte.
Bei einem Widerstandswert von 100 MΩ würde das thermische Rauschen der Quellimpedanz etwa 1,28 µV/√Hz (= 12,8 fA/√Hz) betragen, dann könnte man nicht mehr zwischen dem Stromrauschen des Messobjekts und dem des Widerstands unterscheiden. Falls das Rauschen unkorreliert ist, addieren sich die Rauschsignale geometisch (RSS, root sum squared). Abbildung 4 und Tabelle 1 zeigen die RSS-Summen für verschiedene Verhältnisse von zwei Werten und die entsprechende Zunahme des Gesamtrauschens. Bei einem Verhältnis von n:n nimmt das Rauschen um 41% zu, bei n:n/2 um etwa 12%, bei n:n/3 um etwa 5,5% und bei n:n/5 um etwa 2%. Bei Mittelung über hinreichend viele Zyklen könnten wir auf etwa 10% (0,57 fA/√Hz und 1,28 fA/√Hz RSS) kommen.
Tabelle 1. RSS-Addition auf der Basis des Verhältnisses zweier Werte
| Wert 1 | Wert 2 | RSS-Summe | % Zunahme |
| n | n | 1.414 n | 41.42% |
| n | n/2 | 1.118 n | 11.80% |
| n | n/3 | 1.054 n | 5.41% |
| n | n/4 | 1.031 n | 3.08% |
| n | n/5 | 1.020 n | 2.00% |
| n | n/6 | 1.014 n | 1.38% |
| n | n/7 | 1.010 n | 1.02% |
| n | n/8 | 1.008 n | 0.78% |
| n | n/9 | 1.006 n | 0.62% |
| n | n/10 | 1.005 n | 0.50% |
 Abbildung 5. Ausgangsbezogene Rauschspannungsdichte.
Das Ausgangsspannungsrauschen kann mithilfe eines Dynamiksignalanalysators SR785 oder eines Oszilloskops mit FFT-Funktion gemessen werden; das Grundrauschen des Messgeräts sollte möglichst unter 7 nV/√Hz liegen. Wenn das Ausgangsrauschen des Messobjekts sich mit zunehmender Frequenz dem Wert 20 nV/√Hz bis 30 nV/√Hz nähert, möchten wir, dass das Analysator-Grundrauschen möglichst wenig zum Gesamtrauschen beiträgt. Bei einem Rauschverhältnis von 1:3 erhöht sich das Gesamtrauschen nur um etwa 5.5%. Das ist ein Wert, mit dem man bei Rauschmessungen leben kann (siehe Abbildung 4).
Die Kunst besteht in der Rückrechnung
Bei der beschriebenen Vorgehensweise werden die beiden wichtigsten Parameter, die zur Darstellung des Stromrauschens über der Frequenz benötigt werden, mit einer einzigen Messung erfasst. Zuerst messen wir die Gesamteingangskapazität, bestehend aus der Eingangskapazität des Messobjekts und den Parasitärkapazitäten. Das ist notwendig, damit wir den Roll-off herausrechnen können. Trotz der Parasitärkapazitäten wurde die gesuchte Information erfasst. Die Eingangskapazität dominiert über den 10-GΩ-Widerstand. Diese Gesamtimpedanz wandelt den Rauschstrom in eine Rauschspannung um. Deshalb ist es wichtig, diese Gesamtkapazität zu kennen. Weiter zeigt dieser Wert, ab welcher Frequenz das Stromrauschen zu dominieren beginnt – nämlich dort, wo die Kurve von dem –20 dB/Dekade-Abfall abzuweichen beginnt.
Schauen wir uns das Beispiel in Abbildung 5 an. Der 3-dB-Roll-off-Punkt liegt bei 2,1 Hz. Daraus errechnet sich eine Gesamtkapazität von
Abbildung 5. Ausgangsbezogene Rauschspannungsdichte.
Das Ausgangsspannungsrauschen kann mithilfe eines Dynamiksignalanalysators SR785 oder eines Oszilloskops mit FFT-Funktion gemessen werden; das Grundrauschen des Messgeräts sollte möglichst unter 7 nV/√Hz liegen. Wenn das Ausgangsrauschen des Messobjekts sich mit zunehmender Frequenz dem Wert 20 nV/√Hz bis 30 nV/√Hz nähert, möchten wir, dass das Analysator-Grundrauschen möglichst wenig zum Gesamtrauschen beiträgt. Bei einem Rauschverhältnis von 1:3 erhöht sich das Gesamtrauschen nur um etwa 5.5%. Das ist ein Wert, mit dem man bei Rauschmessungen leben kann (siehe Abbildung 4).
Die Kunst besteht in der Rückrechnung
Bei der beschriebenen Vorgehensweise werden die beiden wichtigsten Parameter, die zur Darstellung des Stromrauschens über der Frequenz benötigt werden, mit einer einzigen Messung erfasst. Zuerst messen wir die Gesamteingangskapazität, bestehend aus der Eingangskapazität des Messobjekts und den Parasitärkapazitäten. Das ist notwendig, damit wir den Roll-off herausrechnen können. Trotz der Parasitärkapazitäten wurde die gesuchte Information erfasst. Die Eingangskapazität dominiert über den 10-GΩ-Widerstand. Diese Gesamtimpedanz wandelt den Rauschstrom in eine Rauschspannung um. Deshalb ist es wichtig, diese Gesamtkapazität zu kennen. Weiter zeigt dieser Wert, ab welcher Frequenz das Stromrauschen zu dominieren beginnt – nämlich dort, wo die Kurve von dem –20 dB/Dekade-Abfall abzuweichen beginnt.
Schauen wir uns das Beispiel in Abbildung 5 an. Der 3-dB-Roll-off-Punkt liegt bei 2,1 Hz. Daraus errechnet sich eine Gesamtkapazität von
 am Eingang. Aus dem Datenblatt zum Messobjekt entnehmen wir, dass dessen Eingangskapazität nur etwa 2,1 pF beträgt. Das bedeutet, dass die Parasitärkapazitäten zusammen etwa 5,5 pF betragen. Die Gegentakt-Eingangskapazität wird mittels Bootstrapping verringert und spielt daher bei niedrigen Frequenzen keine signifikante Rolle. Abbildung 6 zeigt die Gesamtkapazität aus 10 GΩ parallel 7,6 pF, mit der das Stromrauschen "konfrontiert" ist.
am Eingang. Aus dem Datenblatt zum Messobjekt entnehmen wir, dass dessen Eingangskapazität nur etwa 2,1 pF beträgt. Das bedeutet, dass die Parasitärkapazitäten zusammen etwa 5,5 pF betragen. Die Gegentakt-Eingangskapazität wird mittels Bootstrapping verringert und spielt daher bei niedrigen Frequenzen keine signifikante Rolle. Abbildung 6 zeigt die Gesamtkapazität aus 10 GΩ parallel 7,6 pF, mit der das Stromrauschen "konfrontiert" ist.
 Abbildung 6. Betrag der Gesamtimpedanz der Parallelschaltung aus 10-GΩ-Widerstand und 7,6 pF Gesamtkapazität.
Wenn man die am AD8065 gemessene ausgangsbezogene (RTO, referred to output) Rauschspannung (Abbildung 5) durch die frequenzabhängige Impedanz (Abbildung 6) dividiert, erhält man das äquivalente Stromrauschen des AD8065, kombiniert mit dem Stromrauschen des 10-GΩ-Widerstands gemäß RSS (Abbildung 7).
Abbildung 8 zeigt das eingangsbezogene Stromrauschen des AD8065 nach Herausrechnen des Stromrauschens des 10-GΩ-Widerstands. Unterhalb 10 Hz ist die Kurve stark "zerfleddert", weil wir versucht haben, die 0,5 fA/√Hz bis 0,6 fA/√Hz aus 1,28 fA/√Hz (10% auf der RSS-Skala) herauszufischen und nur 100 Mittelungen ausgeführt wurden. Zwischen 15 mHz und 1,56 Hz liegen bei einer Auflösungsbandbreite von 4 mHz nicht weniger als 400 Spektrallinien – dadurch dauert eine einzige Mittelung 256 Sekunden! Für 100 Mittelungen benötigt man demnach 25.600 Sekunden, das sind etwas mehr als 7 Stunden.
Abbildung 6. Betrag der Gesamtimpedanz der Parallelschaltung aus 10-GΩ-Widerstand und 7,6 pF Gesamtkapazität.
Wenn man die am AD8065 gemessene ausgangsbezogene (RTO, referred to output) Rauschspannung (Abbildung 5) durch die frequenzabhängige Impedanz (Abbildung 6) dividiert, erhält man das äquivalente Stromrauschen des AD8065, kombiniert mit dem Stromrauschen des 10-GΩ-Widerstands gemäß RSS (Abbildung 7).
Abbildung 8 zeigt das eingangsbezogene Stromrauschen des AD8065 nach Herausrechnen des Stromrauschens des 10-GΩ-Widerstands. Unterhalb 10 Hz ist die Kurve stark "zerfleddert", weil wir versucht haben, die 0,5 fA/√Hz bis 0,6 fA/√Hz aus 1,28 fA/√Hz (10% auf der RSS-Skala) herauszufischen und nur 100 Mittelungen ausgeführt wurden. Zwischen 15 mHz und 1,56 Hz liegen bei einer Auflösungsbandbreite von 4 mHz nicht weniger als 400 Spektrallinien – dadurch dauert eine einzige Mittelung 256 Sekunden! Für 100 Mittelungen benötigt man demnach 25.600 Sekunden, das sind etwas mehr als 7 Stunden.
 Abbildung 7. RTI-Stromrauschen des AD8065 und eines 10-GΩ-Widerstands.
Warum muss man bis hinab zu 15 mHz messen und dafür so viel Zeit aufwenden? Eine Kapazität von 10 pF ergibt bei einem Widerstand von 10 GΩ ein Tiefpassfilter mit einer Grenzfrequenz von 1,6 Hz. Rauscharme Verstärker mit FET-Eingang haben große Eingangskapazitäten bis zu 20 pF, das ergibt eine –3-dB-Grenzfrequenz von 0,8 Hz. Um den –3-dB-Punkt korrekt messen zu können, müssten wir einen 20-dB-Abfall unterhalb von 0,08 Hz (or 80 mHz) beobachten können.
Eine genauere Analyse des "zerfledderten" Kurvenbereichs unterhalb von 10 Hz ergibt eine Rauschstromdichte von 0,6 fA/√Hz; einen ähnlichen Wert liefert auch die Gleichung
Abbildung 7. RTI-Stromrauschen des AD8065 und eines 10-GΩ-Widerstands.
Warum muss man bis hinab zu 15 mHz messen und dafür so viel Zeit aufwenden? Eine Kapazität von 10 pF ergibt bei einem Widerstand von 10 GΩ ein Tiefpassfilter mit einer Grenzfrequenz von 1,6 Hz. Rauscharme Verstärker mit FET-Eingang haben große Eingangskapazitäten bis zu 20 pF, das ergibt eine –3-dB-Grenzfrequenz von 0,8 Hz. Um den –3-dB-Punkt korrekt messen zu können, müssten wir einen 20-dB-Abfall unterhalb von 0,08 Hz (or 80 mHz) beobachten können.
Eine genauere Analyse des "zerfledderten" Kurvenbereichs unterhalb von 10 Hz ergibt eine Rauschstromdichte von 0,6 fA/√Hz; einen ähnlichen Wert liefert auch die Gleichung
 Diese Gleichung ist demnach bei FETs nicht völlig falsch, sondern zeigt in erster Näherung die niederfrequente Stromrauschcharakteristik des Messobjekts, weil die Messwerte auf dem DC-Eingangsbiasstrom basieren. Bei hohen Frequenzen versagt diese Gleichung jedoch.
Diese Gleichung ist demnach bei FETs nicht völlig falsch, sondern zeigt in erster Näherung die niederfrequente Stromrauschcharakteristik des Messobjekts, weil die Messwerte auf dem DC-Eingangsbiasstrom basieren. Bei hohen Frequenzen versagt diese Gleichung jedoch.
 Abbildung 8. RTI-Stromrauschen des AD8605. / Abbildung 9. RTI-Stromrauschen ausgewählter Verstärker von ADI.
Bei höheren Frequenzen dominiert das Stromrauschen des Messobjekts dasjenige des Widerstands signifikant; deshalb kann letzteres vernachlässigt werden. Abbildung 9 zeigt das eingangsbezogene Stromrauschen diverser Verstärker mit FET-Eingang bei 10 GΩ, gemessen mit der Messanordnung von Abbildung 3. Offenbar ist etwa 100 fA/√Hz bei 100 kHz ein typischer Wert, den man bei den meisten Präzisionsverstärkern erwarten darf.
Abbildung 8. RTI-Stromrauschen des AD8605. / Abbildung 9. RTI-Stromrauschen ausgewählter Verstärker von ADI.
Bei höheren Frequenzen dominiert das Stromrauschen des Messobjekts dasjenige des Widerstands signifikant; deshalb kann letzteres vernachlässigt werden. Abbildung 9 zeigt das eingangsbezogene Stromrauschen diverser Verstärker mit FET-Eingang bei 10 GΩ, gemessen mit der Messanordnung von Abbildung 3. Offenbar ist etwa 100 fA/√Hz bei 100 kHz ein typischer Wert, den man bei den meisten Präzisionsverstärkern erwarten darf.
 Abbildung 10. Eingangsbezogenes Stromrauschen des LTC6268.
Eine Ausnahme stellen die Typen LTC6268/LTC6269 dar, die bei 100 kHz ein Stromrauschen von nur 5,6 fA/√Hz aufweisen. Diese Verstärker eignen sich hervorragend für schnelle Transimpedanz- (TIA) Anwendungen, die große Bandbreite, geringe Eingangskapazität und Biasströme im Femtoampere-Bereich erfordern.
Ist das alles, was es zum Stromrauschen von Verstärkern mit FET-Eingang anzumerken gibt?
Nein. Insgesamt gibt es vier Rauschquellen, die signifikant zum Gesamt-Eingangsstromrauschen in Anwendungen mit hoher Quellimpedanz beitragen. Bisher wurden nur zwei davon behandelt. Abbildung 11 zeigt ein vereinfachtes Modell des Operationsverstärkers aus MT-050, das als gutes Beispiel für die Rauschquellen eines Operationsverstärkers dienen kann.
Abbildung 10. Eingangsbezogenes Stromrauschen des LTC6268.
Eine Ausnahme stellen die Typen LTC6268/LTC6269 dar, die bei 100 kHz ein Stromrauschen von nur 5,6 fA/√Hz aufweisen. Diese Verstärker eignen sich hervorragend für schnelle Transimpedanz- (TIA) Anwendungen, die große Bandbreite, geringe Eingangskapazität und Biasströme im Femtoampere-Bereich erfordern.
Ist das alles, was es zum Stromrauschen von Verstärkern mit FET-Eingang anzumerken gibt?
Nein. Insgesamt gibt es vier Rauschquellen, die signifikant zum Gesamt-Eingangsstromrauschen in Anwendungen mit hoher Quellimpedanz beitragen. Bisher wurden nur zwei davon behandelt. Abbildung 11 zeigt ein vereinfachtes Modell des Operationsverstärkers aus MT-050, das als gutes Beispiel für die Rauschquellen eines Operationsverstärkers dienen kann.
 Abbildung 11. Vereinfachtes Modell eines TIA-Verstärkers einschließlich der wichtigsten Rauschquellen.
Stromrauschen aus dem FET-Eingang (in_dut)
Die Stromrauschkurve hängt von der Topologie der Eingangsstufe des Verstärkers ab. Im Allgemeinen ist die Kurve bei niedrigen Frequenzen flach und steigt mit zunehmender Frequenz an. Siehe Abbildung 8. Ab der Grenzfrequenz des Verstärkers sinkt die Verstärkung, und die Rauschkurve geht in einen –20-dB/Dekade-Verlauf über.
Stromrauschen aus dem Widerstand (in_R)
Diese Rauschkomponente kann man berechnen, indem man das thermischen Spannungsrauschen des Widerstands, en_R, durch die Impedanz des Widerstands R dividiert. 1 MΩ trägt etwa 128 fA/√Hz bei, 10 GΩ etwa 1,28 fA/√Hz.
Abbildung 11. Vereinfachtes Modell eines TIA-Verstärkers einschließlich der wichtigsten Rauschquellen.
Stromrauschen aus dem FET-Eingang (in_dut)
Die Stromrauschkurve hängt von der Topologie der Eingangsstufe des Verstärkers ab. Im Allgemeinen ist die Kurve bei niedrigen Frequenzen flach und steigt mit zunehmender Frequenz an. Siehe Abbildung 8. Ab der Grenzfrequenz des Verstärkers sinkt die Verstärkung, und die Rauschkurve geht in einen –20-dB/Dekade-Verlauf über.
Stromrauschen aus dem Widerstand (in_R)
Diese Rauschkomponente kann man berechnen, indem man das thermischen Spannungsrauschen des Widerstands, en_R, durch die Impedanz des Widerstands R dividiert. 1 MΩ trägt etwa 128 fA/√Hz bei, 10 GΩ etwa 1,28 fA/√Hz.
 Das thermische Spannungsrauschen des Widerstands zeigt bis einer gewissen Frequenz ein völlig flaches Verhalten und geht oberhalb dieser Frequenz allmählich in einen –20-dB/Dekade-Abfall über. Siehe Abbildung 5.
Stromrauschen aus dem Sensor (in_source)
Der Sensor trägt seinen Anteil am Stromrauschen bei, damit müssen wir leben. Der Frequenzverlauf dieser Rauschkomponente kann höchst unterschiedlich sein. Eine Photodiode, beispielsweise, produziert Schrotrauschen, Isn, aus dem Photostrom, IP, und dem Dunkelstrom, ID, sowie Johnson-Rauschen, Ijn, aus dem Shunt-Widerstand.1
Das thermische Spannungsrauschen des Widerstands zeigt bis einer gewissen Frequenz ein völlig flaches Verhalten und geht oberhalb dieser Frequenz allmählich in einen –20-dB/Dekade-Abfall über. Siehe Abbildung 5.
Stromrauschen aus dem Sensor (in_source)
Der Sensor trägt seinen Anteil am Stromrauschen bei, damit müssen wir leben. Der Frequenzverlauf dieser Rauschkomponente kann höchst unterschiedlich sein. Eine Photodiode, beispielsweise, produziert Schrotrauschen, Isn, aus dem Photostrom, IP, und dem Dunkelstrom, ID, sowie Johnson-Rauschen, Ijn, aus dem Shunt-Widerstand.1
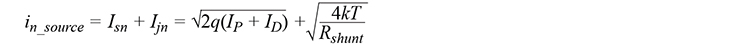 Stromrauschen aus dem Spannungsrauschen des Verstärkers
Das Stromrauschen aus dem Spannungsrauschen des Verstärkers wird als enC-Rauschen bezeichnet und in The Art of Electronics von Horowitz und Hill sehr gut erklärt.2 Ähnlich wie das Spannungsrauschen des Widerstands durch den Widerstand selbst in ein Stromrauschen umgewandelt wird, wird das Spannungsrauschen des Verstärkers, en_dut , durch die Gesamt-Eingangskapazität – die sich aus der Sensorkapazität, den Parasitärkapazitäten der Leiterplatte und der Eingangskapazität des Verstärker zusammensetzt – in Stromrauschen umgewandelt.
Stromrauschen aus dem Spannungsrauschen des Verstärkers
Das Stromrauschen aus dem Spannungsrauschen des Verstärkers wird als enC-Rauschen bezeichnet und in The Art of Electronics von Horowitz und Hill sehr gut erklärt.2 Ähnlich wie das Spannungsrauschen des Widerstands durch den Widerstand selbst in ein Stromrauschen umgewandelt wird, wird das Spannungsrauschen des Verstärkers, en_dut , durch die Gesamt-Eingangskapazität – die sich aus der Sensorkapazität, den Parasitärkapazitäten der Leiterplatte und der Eingangskapazität des Verstärker zusammensetzt – in Stromrauschen umgewandelt.
 Zunächst erhalten wir:
Zunächst erhalten wir:
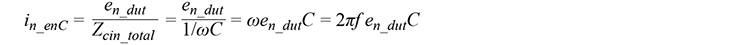 Diese Gleichung lehrt uns drei Dinge. Erstens: Das Stromrauschen wird mit zunehmender Frequenz stärker – noch eine weitere Komponente des Stromrauschens, die diese Eigenschaft aufweist. Zweitens: Je größer das Eingangsspannungsrauschen des Verstärkers ist, desto größer auch das Stromrauschen. Drittens: Je größer die Gesamt-Eingangskapazität ist, desto größer ist auch das Stromrauschen. Das führt zu einer Gütezahl ("figure of merit") enC, die in einer gegeben Anwendung sowohl das Spannungsrauschen des Verstärkers als auch die Gesamt-Eingangskapazität berücksichtigt.
Abbildung 12 zeigt die Stromrauschkurve für TIA-Anwendungen, die das Stromrauschen des Messobjekts vernachlässigt. Der flache Teil der Kurve beschreibt im Wesentlichen das Widerstandsrauschen.
Diese Gleichung lehrt uns drei Dinge. Erstens: Das Stromrauschen wird mit zunehmender Frequenz stärker – noch eine weitere Komponente des Stromrauschens, die diese Eigenschaft aufweist. Zweitens: Je größer das Eingangsspannungsrauschen des Verstärkers ist, desto größer auch das Stromrauschen. Drittens: Je größer die Gesamt-Eingangskapazität ist, desto größer ist auch das Stromrauschen. Das führt zu einer Gütezahl ("figure of merit") enC, die in einer gegeben Anwendung sowohl das Spannungsrauschen des Verstärkers als auch die Gesamt-Eingangskapazität berücksichtigt.
Abbildung 12 zeigt die Stromrauschkurve für TIA-Anwendungen, die das Stromrauschen des Messobjekts vernachlässigt. Der flache Teil der Kurve beschreibt im Wesentlichen das Widerstandsrauschen.
 Das kapazitätsbedingte Stromrauschen berechnet sich nach folgender Gleichung:
Das kapazitätsbedingte Stromrauschen berechnet sich nach folgender Gleichung:
 Es steigt um 20 dB/Dekade an. Aus den beiden Gleichungen lässt sich der Schnittpunkt berechnen:
Es steigt um 20 dB/Dekade an. Aus den beiden Gleichungen lässt sich der Schnittpunkt berechnen:
 Je nach Cin kann das enC-Rauschen größer oder kleiner als das Stromrauschen des Messobjekts sein. Bei invertierenden Schaltungen, beispielsweise in TIA-Anwendungen, wird Cdm nicht "gebootstrapped"; es gilt
Je nach Cin kann das enC-Rauschen größer oder kleiner als das Stromrauschen des Messobjekts sein. Bei invertierenden Schaltungen, beispielsweise in TIA-Anwendungen, wird Cdm nicht "gebootstrapped"; es gilt
 Für den LTC6244, beispielsweise, gelten bei 100 kHz die folgenden Werte: Ccm = 2,1 pF, Cdm = 3,5 pF und en = 8 nV/√Hz. Daraus berechnet sich ein enC-Stromrauschen von
Für den LTC6244, beispielsweise, gelten bei 100 kHz die folgenden Werte: Ccm = 2,1 pF, Cdm = 3,5 pF und en = 8 nV/√Hz. Daraus berechnet sich ein enC-Stromrauschen von
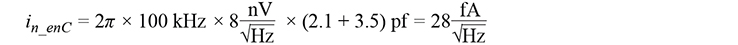 Dieser Wert ist wesentlich kleiner als das Stromrauschen des Messobjekts von 80 fA/vHz
Dieser Wert ist wesentlich kleiner als das Stromrauschen des Messobjekts von 80 fA/vHz
 Abbildung 12. enC-Rauschen über der Frequenz.
Wenn jedoch eine Photodiode angeschlossen ist, ist eine zusätzliche Kapazität Csource oder Cpd zur Gleichung hinzu zu addieren, und das Stromrauschen muss neu berechnet werden. Schon bei einer kleinen Cpd-Kapazität von nur 16 pF steigt das enC-Stromrauschen auf ähnliche Werte wie das Stromrauschen des Messobjekts an. Langsame, großflächige Photodioden haben meistens Kapazitäten in der Größenordnung von 100 pF bis 1 nF, kleinflächige High-Speed-Typen dagegen Werte von etwa 1 pF bis 10 pF.
Zusammenfassung
Das Phänomen, dass sowohl bei Verstärkern mit CMOS- als auch solchen mit JFET-Eingang das Stromrauschen mit ansteigender Frequenz zunimmt, ist IC-Designern und erfahrenen Schaltungsentwicklern bekannt. Es war vielen Ingenieuren jedoch nicht zugänglich, weil es entweder zu wenige Fachartikel auf diesem Gebiet gab oder weil die Informationen der Halbleiterhersteller unvollständig waren. Ziel dieses Artikel ist es, zu einem besseren Verständnis des Stromrauschens bei höheren Frequenzen beizutragen und eine Technik für reproduzierbare Rauschmessungen am Operationsverstärker der Wahl zu beschreiben.
Weiterführende Informationen
Die Auswahl des für eine gegebene Anwendung optimalen Operationsverstärkers ist keine einfache Aufgabe. Je nach Anwendung muss man Kompromisse zwischen Rauschen, Bandbreite, Verstärkung und Genauigkeit eingehen. Die untenstehenden Literaturhinweise 1, 2, 3, 4, 5, 6 und 7 sowie zahlreiche Datenblätter informieren ausführlich darüber, was dabei zu beachten ist.
Literaturhinweise
Abbildung 12. enC-Rauschen über der Frequenz.
Wenn jedoch eine Photodiode angeschlossen ist, ist eine zusätzliche Kapazität Csource oder Cpd zur Gleichung hinzu zu addieren, und das Stromrauschen muss neu berechnet werden. Schon bei einer kleinen Cpd-Kapazität von nur 16 pF steigt das enC-Stromrauschen auf ähnliche Werte wie das Stromrauschen des Messobjekts an. Langsame, großflächige Photodioden haben meistens Kapazitäten in der Größenordnung von 100 pF bis 1 nF, kleinflächige High-Speed-Typen dagegen Werte von etwa 1 pF bis 10 pF.
Zusammenfassung
Das Phänomen, dass sowohl bei Verstärkern mit CMOS- als auch solchen mit JFET-Eingang das Stromrauschen mit ansteigender Frequenz zunimmt, ist IC-Designern und erfahrenen Schaltungsentwicklern bekannt. Es war vielen Ingenieuren jedoch nicht zugänglich, weil es entweder zu wenige Fachartikel auf diesem Gebiet gab oder weil die Informationen der Halbleiterhersteller unvollständig waren. Ziel dieses Artikel ist es, zu einem besseren Verständnis des Stromrauschens bei höheren Frequenzen beizutragen und eine Technik für reproduzierbare Rauschmessungen am Operationsverstärker der Wahl zu beschreiben.
Weiterführende Informationen
Die Auswahl des für eine gegebene Anwendung optimalen Operationsverstärkers ist keine einfache Aufgabe. Je nach Anwendung muss man Kompromisse zwischen Rauschen, Bandbreite, Verstärkung und Genauigkeit eingehen. Die untenstehenden Literaturhinweise 1, 2, 3, 4, 5, 6 und 7 sowie zahlreiche Datenblätter informieren ausführlich darüber, was dabei zu beachten ist.
Literaturhinweise
- 1 Photodiode Characteristics und Applications. OSI Optoelectronics, August 2007.
- 2 Paul Horowitz und Winfield Hill. The Art of Electronics, 3. Auflage. Cambridge University Press, April 2015.
- 3 ADA4530-1 Data Sheet. Analog Devices, Inc., November 2019.
- 4 CN-0407. Analog Devices, Inc., Februar 2019.
- 5 “ADA4530-1R-EBZ User Guide: UG-865.” Analog Devices, Inc., Oktober 2015.
- 6 “MT-050: Op Amp Total Output Noise Calculations for Second-Order System.” Analog Devices, Inc., Februar 2009.
- 7 Low Level Measurements Handbook: Precision DC Current, Voltage und Resistance Measurements. Tektronix, Inc., Februar 2016.
- Brisebois, Glen. “Signal Conditioning for High Impedance Sensors.” Analog Devices, Inc..
- Brisebois, Glen. “Transimpedance Amplifier Noise Considerations.” Analog Devices, Inc..
 Abbildung 13. Messanordnung..
Bei einem typischen IC mit einem einzigen Verstärker befindet sich Pin3 (Vin+) unmittelbar neben Pin4 (V–). Falls kein Guard-Ring vorhanden ist, spielt das Leiterplattenlayout eine entscheidende Rolle. Bei Betriebsspannungsänderungen änderte sich auch der Gleichspannungsanteil der Ausgangsspannung signifikant. Der 10-GΩ-SMD-Widerstand war ursprünglich parallel zu V– (R10 in Abbildung 13) eingelötet, und der Leckstrom durch die Lotpaste war inakzeptabel. Deshalb wurde der 10-GΩ-SMD-Widerstand an anderer Stelle angebracht (R8), woraufhin der Leckstrom verschwand. Das Datenblatt zum ADA4530-1 (Verstärker der Elektrometerklasse mit 20 fA bei 85°C) beschreibt alle Vorkehrungen hinsichtlich Auswahl der Lotpaste, Verschmutzung, Feuchtigkeit und anderer Einflussgrößen, die bei Hochimpedanzmessungen getroffen werden müssen. Es lohnt sich, das Datenblatt und den User Guide UG-865 sowie die Circuit Note CN-0407 zu lesen.
Nicht-schallisolierte Bauteile mit hoher Eingangsimpedanz können triboelektrischen, piezoelektrischen und mikrophonischen Effekten unterliegen. Irgendwann einmal habe ich unbeabsichtigt meinen Schlüsselbund fallen lassen und bemerkte im Messdiagramm einen Spike im hörbaren Frequenzbereich (insbesondere 1 kHz und darüber). Ich hätte nicht gedacht, dass Messungen an einer hochimpedanten FET-Eingangsstufe mit 10 GΩ Eingangswiderstand derart schallempfindlich sein könnten. Um mich zu vergewissern, pfiff ich – und siehe da, ich bekam einen Spike zwischen 1 kHz und 2 kHz zu sehen. Selbst bei Messdatenmittelung über zahlreiche Zyklen genügt ein kurzes Pfeifen, um im CRT-Diagramm des SR785 einen Spike hervorzurufen. Die in CN-0407 erwähnten, hermetisch dichten Glaswiderstände wären im Hinblick auf tribo-/piezoelektrische Effekte eine bessere Wahl.
Abbildung 13. Messanordnung..
Bei einem typischen IC mit einem einzigen Verstärker befindet sich Pin3 (Vin+) unmittelbar neben Pin4 (V–). Falls kein Guard-Ring vorhanden ist, spielt das Leiterplattenlayout eine entscheidende Rolle. Bei Betriebsspannungsänderungen änderte sich auch der Gleichspannungsanteil der Ausgangsspannung signifikant. Der 10-GΩ-SMD-Widerstand war ursprünglich parallel zu V– (R10 in Abbildung 13) eingelötet, und der Leckstrom durch die Lotpaste war inakzeptabel. Deshalb wurde der 10-GΩ-SMD-Widerstand an anderer Stelle angebracht (R8), woraufhin der Leckstrom verschwand. Das Datenblatt zum ADA4530-1 (Verstärker der Elektrometerklasse mit 20 fA bei 85°C) beschreibt alle Vorkehrungen hinsichtlich Auswahl der Lotpaste, Verschmutzung, Feuchtigkeit und anderer Einflussgrößen, die bei Hochimpedanzmessungen getroffen werden müssen. Es lohnt sich, das Datenblatt und den User Guide UG-865 sowie die Circuit Note CN-0407 zu lesen.
Nicht-schallisolierte Bauteile mit hoher Eingangsimpedanz können triboelektrischen, piezoelektrischen und mikrophonischen Effekten unterliegen. Irgendwann einmal habe ich unbeabsichtigt meinen Schlüsselbund fallen lassen und bemerkte im Messdiagramm einen Spike im hörbaren Frequenzbereich (insbesondere 1 kHz und darüber). Ich hätte nicht gedacht, dass Messungen an einer hochimpedanten FET-Eingangsstufe mit 10 GΩ Eingangswiderstand derart schallempfindlich sein könnten. Um mich zu vergewissern, pfiff ich – und siehe da, ich bekam einen Spike zwischen 1 kHz und 2 kHz zu sehen. Selbst bei Messdatenmittelung über zahlreiche Zyklen genügt ein kurzes Pfeifen, um im CRT-Diagramm des SR785 einen Spike hervorzurufen. Die in CN-0407 erwähnten, hermetisch dichten Glaswiderstände wären im Hinblick auf tribo-/piezoelektrische Effekte eine bessere Wahl.
 Abbildung 14. Akustische Geräusche im Labor. / Abbildung 15. Akustische Geräusche in der Telefonkabine.
Um der Sache auf den Grund zu gehen, habe ich die Geräusche im Labor mithilfe eines Laptop-Mikrofons aufgenommen, die Messdaten mithilfe von MATLAB® analysiert und herausgefunden, dass die Rauschmessungen mit den Umgebungsgeräuschen korreliert waren. Ein signifikanter, geräuschbedingter Spike trat bei 768 Hz und weiteren Frequenzen auf (siehe Abbildung 14). Verantwortlich dafür war ein großer Netzspannungskabelschacht in ein paar Metern Entfernung von meinem Labortisch. Um sicherzugehen, nicht auch noch das Betriebsgeräusch meines Laptops zu erfassen, ging ich für die Messungen in eine der Telefonkabinen – das sind die ruhigsten Plätze in meiner Arbeitsumgebung. Bei 768 Hz war daraufhin kein Spike mehr zu erkennen, und die Spikes bei anderen Frequenzen waren um mindestens den Faktor 100 kleiner.
Abbildung 14. Akustische Geräusche im Labor. / Abbildung 15. Akustische Geräusche in der Telefonkabine.
Um der Sache auf den Grund zu gehen, habe ich die Geräusche im Labor mithilfe eines Laptop-Mikrofons aufgenommen, die Messdaten mithilfe von MATLAB® analysiert und herausgefunden, dass die Rauschmessungen mit den Umgebungsgeräuschen korreliert waren. Ein signifikanter, geräuschbedingter Spike trat bei 768 Hz und weiteren Frequenzen auf (siehe Abbildung 14). Verantwortlich dafür war ein großer Netzspannungskabelschacht in ein paar Metern Entfernung von meinem Labortisch. Um sicherzugehen, nicht auch noch das Betriebsgeräusch meines Laptops zu erfassen, ging ich für die Messungen in eine der Telefonkabinen – das sind die ruhigsten Plätze in meiner Arbeitsumgebung. Bei 768 Hz war daraufhin kein Spike mehr zu erkennen, und die Spikes bei anderen Frequenzen waren um mindestens den Faktor 100 kleiner.
 Abbildung 16. Ausgangsbezogene Spannungsrauschdichte ohne akustische Abschirmung. / Abbildung 17. Ausgangsbezogene Spannungsrauschdichte mit akustischer Abschirmung.
Zur Dämpfung der akustischen Geräusche verwendete ich daraufhin eine Temptronix-Box. Die Box scheint temperaturgedämmt zu sein, eine signifikante Luftbewegung findet darin nicht statt. Darauf kam es mir aber nicht an. Es ging mir nur darum, die Messanordnung vor Schall zu schützen – und das tat die Box. Siehe Abbildungen 16 und 17.
Fehlerquellen, an die man vielleicht nicht denkt
Abbildung 16. Ausgangsbezogene Spannungsrauschdichte ohne akustische Abschirmung. / Abbildung 17. Ausgangsbezogene Spannungsrauschdichte mit akustischer Abschirmung.
Zur Dämpfung der akustischen Geräusche verwendete ich daraufhin eine Temptronix-Box. Die Box scheint temperaturgedämmt zu sein, eine signifikante Luftbewegung findet darin nicht statt. Darauf kam es mir aber nicht an. Es ging mir nur darum, die Messanordnung vor Schall zu schützen – und das tat die Box. Siehe Abbildungen 16 und 17.
Fehlerquellen, an die man vielleicht nicht denkt
 Abbildung 18. Externes Hochpassfilter, zur Minimierung der Störsignale aus dem Analysatorbildschirm gedreht.
Verstärker mit FET-Eingang haben Eingangsströme in der Größenordnung von pA. Bei einem Eingangswiderstand von 10 GΩ produziert ein Eingangsstrom von 10 pA am Verstärkerausgang eine Offsetspannung von 100 mV. Der Eingang des SR785 bietet die Wahl zwischen DC- und AC-Kopplung. In Stellung AC wird dieser Offset ausgeblendet, und man kann das Ausgangsrauschen im Messbereich höchster Empfindlichkeit (–50 dBV-Spitze bzw. 3,2 mV-Spitze) messen. Durch die AC-Kopplung wird jedoch der Frequenzbereich auf eine untere Grenzfrequenz von 1 Hz beschnitten; dadurch ist es schwierig, den flachen 12,8-µV/√Hz-Bereich zu analysieren und den –3 dB-Punkt zu messen.
Deshalb muss man mit DC-Kopplung arbeiten, mit der Folge, dass der empfindlichste Messbereich des Analysators nicht genutzt werden kann. Dieses Problem wurde gelöst, indem dem Eingang des SR785 ein Hochpassfilter mit 1 mHz Grenzfrequenz – bestehend aus zwei polarisierten, in Serie geschalteten 270-µF-Kondensatoren (Gesamtkapazität 135 µF) und einem 1-MΩ-Widerstand – vorgeschaltet wurde. Der Bildschirm des SR785 produziert ein Magnetfeld mit Frequenzen im Bereich von 20 kHz und Oberwellen, das in den Kondensatoren des externen Hochpassfilters Störsignale hervorrufen kann. Diese lassen sich durch Drehen des Filters (blaue Box) minimieren (siehe Abbildung 18).
Über den Autor: Kaung Win begann seine Laufbahn bei Analog Devices im Jahr 2013 als Produkterprobungsingenieur für die Linear Products and Solutions Group. Im Jahr 2019 wechselte er auf eine Stelle als Anwendungsingenieur. Er hat einen Bachelor-Abschluss in Elektro- und Computertechnik vom Worcester Polytechnic Institute und einen Master-Abschluss in Elektrotechnik von der Universität Santa Clara. Sein Spezialgebiet sind Lösungen für die Verstärker-Signalkette. Kaung ist unter kaung.win@analog.com. zu erreichen. / Copyright: © Analog Devices Inc.
Abbildung 18. Externes Hochpassfilter, zur Minimierung der Störsignale aus dem Analysatorbildschirm gedreht.
Verstärker mit FET-Eingang haben Eingangsströme in der Größenordnung von pA. Bei einem Eingangswiderstand von 10 GΩ produziert ein Eingangsstrom von 10 pA am Verstärkerausgang eine Offsetspannung von 100 mV. Der Eingang des SR785 bietet die Wahl zwischen DC- und AC-Kopplung. In Stellung AC wird dieser Offset ausgeblendet, und man kann das Ausgangsrauschen im Messbereich höchster Empfindlichkeit (–50 dBV-Spitze bzw. 3,2 mV-Spitze) messen. Durch die AC-Kopplung wird jedoch der Frequenzbereich auf eine untere Grenzfrequenz von 1 Hz beschnitten; dadurch ist es schwierig, den flachen 12,8-µV/√Hz-Bereich zu analysieren und den –3 dB-Punkt zu messen.
Deshalb muss man mit DC-Kopplung arbeiten, mit der Folge, dass der empfindlichste Messbereich des Analysators nicht genutzt werden kann. Dieses Problem wurde gelöst, indem dem Eingang des SR785 ein Hochpassfilter mit 1 mHz Grenzfrequenz – bestehend aus zwei polarisierten, in Serie geschalteten 270-µF-Kondensatoren (Gesamtkapazität 135 µF) und einem 1-MΩ-Widerstand – vorgeschaltet wurde. Der Bildschirm des SR785 produziert ein Magnetfeld mit Frequenzen im Bereich von 20 kHz und Oberwellen, das in den Kondensatoren des externen Hochpassfilters Störsignale hervorrufen kann. Diese lassen sich durch Drehen des Filters (blaue Box) minimieren (siehe Abbildung 18).
Über den Autor: Kaung Win begann seine Laufbahn bei Analog Devices im Jahr 2013 als Produkterprobungsingenieur für die Linear Products and Solutions Group. Im Jahr 2019 wechselte er auf eine Stelle als Anwendungsingenieur. Er hat einen Bachelor-Abschluss in Elektro- und Computertechnik vom Worcester Polytechnic Institute und einen Master-Abschluss in Elektrotechnik von der Universität Santa Clara. Sein Spezialgebiet sind Lösungen für die Verstärker-Signalkette. Kaung ist unter kaung.win@analog.com. zu erreichen. / Copyright: © Analog Devices Inc.

