
© Analog Devices Inc.
Application Notes |
Erstellen physikalisch genauer Makromodelle für Analogschalter
Frage: Kann ich das LTspice®-Modell eines Analogschalters verbessern, wenn mein analoges Design Schalter und Multiplexer enthält?
Antwort: Sicher, das Erstellen eigener Modelle ist nicht schwer.
Ich habe eine Schaltung getestet und dabei viele Abweichungen vom Papierentwurf festgestellt, den ich zur Erstellung verwendet hatte. Die Dynamik der Schaltung war etwas unerwartet, und der Rauschpegel war viel größer als gefordert. Ich musste die Schaltung mit einem Simulator untersuchen, um sie vollständig zu verstehen.
Die Schaltung bestand aus Analogschaltern und Operationsverstärkern. Es sind gute Makromodelle für die verwendeten Operationsverstärker vorhanden, aber das Makromodel für die Analogschalter wurde nicht für die Allgemeinheit konzipiert. Der Header der Makromodelldatei des Schalters enthält die Warnung, dass die modellierten Parameter nur für eine bestimmte Versorgungsspannung und Temperatur gültig sind. Nun, wer hätte das gedacht: Meine Schaltung hat andere Betriebsbedingungen als die modellierte. Die Sache mit Analogschaltern ist, dass diese so universell einsetzbar sind, dass ein Arbeitspunkt nicht ausreicht. Die vorhandenen Industrie-Standardmodelle liefern einen guten Ausgangspunkt, aber im analogen Hochleistungsbereich ist möglicherweise ein neuer Modellierungsansatz erforderlich, der Ihre Simulation auf ein höheres Niveau bringt.
Als ich damit begann, verschiedene Analogschalter-Makromodelle von Analog Devices und anderen IC-Herstellern zu durchstöbern, fiel mir auf, dass in allen ihren Headern angegeben ist, dass keine Versorgungsspannungs- oder Temperaturabhängigkeit modelliert wird. Ich musste daher mein eigenes Makromodell erstellen.
Meine Philosophie in dieser Arbeit besteht darin, dass Volltransistoren in den Analogschaltern, die die einfachsten Bauteilmodelle verwenden, zwar sämtliche zu emulierenden Verhalten liefern, die Schnittstelle vom Steuerpin zu den MOS-Gattern jedoch aus den einfachsten, verhaltensmodellierten Komponenten bestehen sollte.
Alle Arbeiten hier werden mit dem LTspice-Simulator durchgeführt; der Code würde mittels Übersetzung der LTspice-Verhaltenskomponenten in SPICE-ähnliche Polynomfunktionen aber auch auf anderen Simulatoren funktionieren.
Wir werden die simulierten Verhaltensweisen in einer bestimmten Reihenfolge erarbeiten.
Entwicklung von LTspice-Modellparametern für den On-Widerstand
Für den Betrieb realer MOS-Bausteine verwenden wir das einfachste Modell. Zur Modellierung des On-Widerstands verwenden wir die folgenden Parameter:
Betrachten wir einmal die RON-Kurven für ADG333A, die wir in Abbildung 1 wiedergeben möchten.
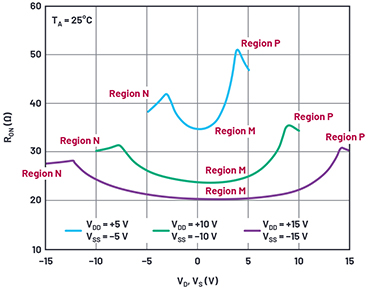 Abbildung 1. RON in Abhängigkeit von VD (VS), duale Spannungsversorgung.
Es ist als allgemeiner Trend für diesen und alle anderen Analogschalter zu erkennen, dass höhere Versorgungsspannungen den On-Widerstand verringern. Je höher die an die MOS-Gates des Schalters angelegte Spannung ist, desto geringer wird der On-Widerstand. Zu beobachten auch eine deutliche Veränderung des Widerstands über den analogen Pegel. In den N-Regionen ist der NMOS-Transistor eines Schalters vollständig eingeschaltet. Wenn die Analogspannung über die negative Linie ansteigt, schaltet sich der PMOS-Transistor ein und trägt zur Verringerung des Gesamt-On-Widerstands bei. Der Wendepunkt in der N-Region liegt ungefähr eine PMOS VTO über der negativen Versorgungsspannung.
In gleicher Weise ist in den P-Regionen der PMOS-Baustein des Schalters vollständig eingeschaltet, und der NMOS beginnt, den PMOS-Transistor ungefähr ab einer NMOS-VTO unterhalb der positiven Versorgungsspannung zu unterstützen.
Die M-Regionen befinden sich in der Mitte der N- und P-Regionen, in welcher der NMOS und der PMOS parallel arbeiten, aber je nach dem analogen Signalpegel zwischen den Versorgungen einen unterschiedlichen On-Widerstand aufweisen.
Um mit der Kurvenanpassung zu beginnen, schätzen wir zunächst die Größe eines jeden einzelnen Transistors. Die Kleinspannungskurve liefert die beste Kurvenanpassung für RDS,ON des Transistors. In Region N, mit dem Analogsignal an der negativen Versorgungsspannung, ist das PMOS-Bauelement ausgeschaltet und RON des Bauteils ist gleich dem RON des NMOS-Transistors. Mit
Abbildung 1. RON in Abhängigkeit von VD (VS), duale Spannungsversorgung.
Es ist als allgemeiner Trend für diesen und alle anderen Analogschalter zu erkennen, dass höhere Versorgungsspannungen den On-Widerstand verringern. Je höher die an die MOS-Gates des Schalters angelegte Spannung ist, desto geringer wird der On-Widerstand. Zu beobachten auch eine deutliche Veränderung des Widerstands über den analogen Pegel. In den N-Regionen ist der NMOS-Transistor eines Schalters vollständig eingeschaltet. Wenn die Analogspannung über die negative Linie ansteigt, schaltet sich der PMOS-Transistor ein und trägt zur Verringerung des Gesamt-On-Widerstands bei. Der Wendepunkt in der N-Region liegt ungefähr eine PMOS VTO über der negativen Versorgungsspannung.
In gleicher Weise ist in den P-Regionen der PMOS-Baustein des Schalters vollständig eingeschaltet, und der NMOS beginnt, den PMOS-Transistor ungefähr ab einer NMOS-VTO unterhalb der positiven Versorgungsspannung zu unterstützen.
Die M-Regionen befinden sich in der Mitte der N- und P-Regionen, in welcher der NMOS und der PMOS parallel arbeiten, aber je nach dem analogen Signalpegel zwischen den Versorgungen einen unterschiedlichen On-Widerstand aufweisen.
Um mit der Kurvenanpassung zu beginnen, schätzen wir zunächst die Größe eines jeden einzelnen Transistors. Die Kleinspannungskurve liefert die beste Kurvenanpassung für RDS,ON des Transistors. In Region N, mit dem Analogsignal an der negativen Versorgungsspannung, ist das PMOS-Bauelement ausgeschaltet und RON des Bauteils ist gleich dem RON des NMOS-Transistors. Mit
 setzen wir unter Verwendung der typischen 40-V-NMOS-Prozesswerte aus der Kurve in Abbildung 1 einen RDS,ON = 38 Ω, und unter Verwendung der angegebenen Prozessgrößen finden wir WNMOS = 2 µA/(38 Ω × (11 × 10-6 µA/V2) × (10 V - 0,7 V)) = 514 µm. Der PMOS-Schalter hätte somit einen On-Widerstand von 47 Ω aus der obigen Kurve und damit eine Breite von 936 µm.
setzen wir unter Verwendung der typischen 40-V-NMOS-Prozesswerte aus der Kurve in Abbildung 1 einen RDS,ON = 38 Ω, und unter Verwendung der angegebenen Prozessgrößen finden wir WNMOS = 2 µA/(38 Ω × (11 × 10-6 µA/V2) × (10 V - 0,7 V)) = 514 µm. Der PMOS-Schalter hätte somit einen On-Widerstand von 47 Ω aus der obigen Kurve und damit eine Breite von 936 µm.
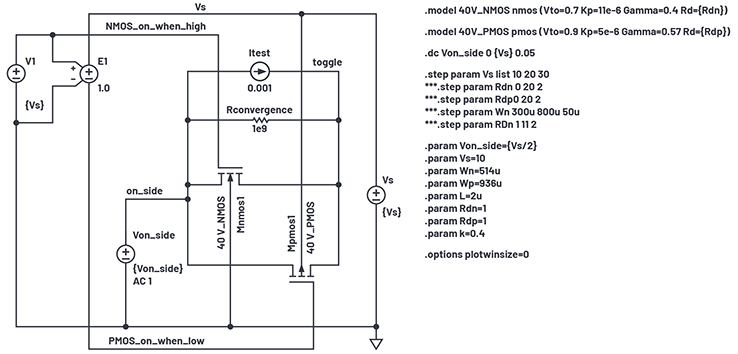 Abbildung 2. Testschaltung für den On-Widerstand
Ich habe die in Abbildung 2 gezeigte LTspice -Testschaltung verwendet. Zu beachten ist, dass die Parameter RDN und RDP, die parasitären Drain-Widerstände, einen eher moderaten Wert haben. Ich habe mit einem Wert von 1 µ begonnen, was zu einer Verlangsamung der Simulatorkonvergenz führte. Ein RDN-Wert von 1 ermöglicht eine angemessene Simulationsgeschwindigkeit. Das Hinzufügen von RCONVERGENCE hat das Simulationsrauschen und die Simulationsgeschwindigkeit verbessert, indem dem Umschaltknoten eine konvergenzfähige Leitfähigkeit verliehen wurde. Für die Messung des On-Widerstands habe ich eine potentialfreie Stromquelle getestet.
Abbildung 2. Testschaltung für den On-Widerstand
Ich habe die in Abbildung 2 gezeigte LTspice -Testschaltung verwendet. Zu beachten ist, dass die Parameter RDN und RDP, die parasitären Drain-Widerstände, einen eher moderaten Wert haben. Ich habe mit einem Wert von 1 µ begonnen, was zu einer Verlangsamung der Simulatorkonvergenz führte. Ein RDN-Wert von 1 ermöglicht eine angemessene Simulationsgeschwindigkeit. Das Hinzufügen von RCONVERGENCE hat das Simulationsrauschen und die Simulationsgeschwindigkeit verbessert, indem dem Umschaltknoten eine konvergenzfähige Leitfähigkeit verliehen wurde. Für die Messung des On-Widerstands habe ich eine potentialfreie Stromquelle getestet.
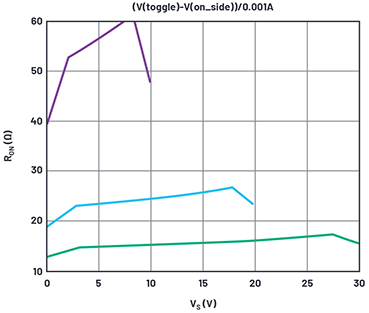 Abbildung 3. Simulationsergebnisse für den On-Widerstand mit anfänglichen Modellwerten.
Abbildung 3 zeigt die Simulationsergebnisse für verschiedene Versorgungsspannungen.
Dies ist schon mal ein guter Anfang. Der Knick am unteren Ende des Spannungsbereichs für VS = 30 V liegt bei 3,6 V in der Simulation und bei 2,7 V im Datenblatt. Dies legt nahe, den PMOS-VTO-Wert zu reduzieren, allerdings ist 0,9 V bereits ein realistisches Minimum. Besser ist es daher, den Gamma-Wert des PMOS anzupassen, der ohnehin nur ein Schätzwert war.
Der Knick in der Nähe der maximalen Versorgungsspannung liegt 2,5 V unterhalb der 30-V-Versorgungsspannung, während er im Datenblatt ~1 V betragen sollte. Verschiedene Gamma-Werte führten zu einer Überhöhung der Knickspannung von der Versorgungsspannung; wir setzen daher einfach die NMOS-VTO auf 1 V und dessen Gamma auf null. Ein Gamma von Null ist nicht zu erwarten, aber wir versuchen nur, uns der Kurve anzupassen.
Abbildung 3. Simulationsergebnisse für den On-Widerstand mit anfänglichen Modellwerten.
Abbildung 3 zeigt die Simulationsergebnisse für verschiedene Versorgungsspannungen.
Dies ist schon mal ein guter Anfang. Der Knick am unteren Ende des Spannungsbereichs für VS = 30 V liegt bei 3,6 V in der Simulation und bei 2,7 V im Datenblatt. Dies legt nahe, den PMOS-VTO-Wert zu reduzieren, allerdings ist 0,9 V bereits ein realistisches Minimum. Besser ist es daher, den Gamma-Wert des PMOS anzupassen, der ohnehin nur ein Schätzwert war.
Der Knick in der Nähe der maximalen Versorgungsspannung liegt 2,5 V unterhalb der 30-V-Versorgungsspannung, während er im Datenblatt ~1 V betragen sollte. Verschiedene Gamma-Werte führten zu einer Überhöhung der Knickspannung von der Versorgungsspannung; wir setzen daher einfach die NMOS-VTO auf 1 V und dessen Gamma auf null. Ein Gamma von Null ist nicht zu erwarten, aber wir versuchen nur, uns der Kurve anzupassen.
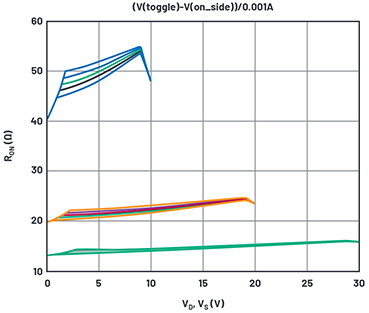 Abbildung 4. Simulationsergebnisse für den On-Widerstand bei Variation von gamma-p
Abbildung 4 zeigt die Simulationsergebnisse aus diesen Werten, wobei der Gamma-Wert des PMOS für verschiedene Versorgungsspannungen stufenweise erhöht wurde. Wir konzentrieren uns auf die 30-V-Kurven, bei denen der Gamma-Effekt maximal ist im Vergleich zu niedrigeren Versorgungsspannungen
Aus den abgestuften Kurven wählen wir ein PMOS-Gamma = 0,4.
Weiter zu RON. Es ist zu beachten, dass die 10 V-Kurven repräsentativ für die Datenblattkurve an den Extrema der Versorgungsspannung sind, die Simulation jedoch einen zu niedrigen RON für die 20-V- und 30-V-Kurven ergibt. Die RONs entsprechen RDS,ON(NMOS) + RD(NMOS) im Bereich nahe der positiven Versorgungsspannung und RDS,ON(PMOS) + RD(PMOS) Im Bereich nahe der positiven Versorgungsspannung. Bei hohen Versorgungsspannungen ist der Parameter RD signifikanter als W/L, während bei niedrigen Versorgungsspannungen W/L dominiert.
Abbildung 4. Simulationsergebnisse für den On-Widerstand bei Variation von gamma-p
Abbildung 4 zeigt die Simulationsergebnisse aus diesen Werten, wobei der Gamma-Wert des PMOS für verschiedene Versorgungsspannungen stufenweise erhöht wurde. Wir konzentrieren uns auf die 30-V-Kurven, bei denen der Gamma-Effekt maximal ist im Vergleich zu niedrigeren Versorgungsspannungen
Aus den abgestuften Kurven wählen wir ein PMOS-Gamma = 0,4.
Weiter zu RON. Es ist zu beachten, dass die 10 V-Kurven repräsentativ für die Datenblattkurve an den Extrema der Versorgungsspannung sind, die Simulation jedoch einen zu niedrigen RON für die 20-V- und 30-V-Kurven ergibt. Die RONs entsprechen RDS,ON(NMOS) + RD(NMOS) im Bereich nahe der positiven Versorgungsspannung und RDS,ON(PMOS) + RD(PMOS) Im Bereich nahe der positiven Versorgungsspannung. Bei hohen Versorgungsspannungen ist der Parameter RD signifikanter als W/L, während bei niedrigen Versorgungsspannungen W/L dominiert.
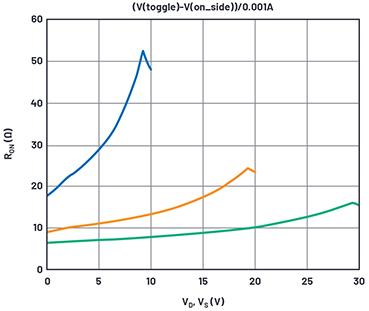 Abbildung 5. Simulationsergebnisse für den On-Widerstand mit festgelegtem WN.
Wir müssen hier mit zwei Variablen jonglieren, was zu mühsam ist. Es ist festzustellen, dass sich der RON-Wert mit der Versorgungsspannung ändert, weil der NMOS variabel angereichert wird, der RD-Wert sich jedoch nicht mit der Versorgungsspannung ändert (okay, bei Drains mit Drift-Regionen tut er dies wahrscheinlich doch, aber wir wollen es hier einfach halten).
Wenn wir den Unterschied für RON im Datenblatt zwischen den Versorgungsspannungen 10 V und 30 V beachten (11,4 Ω), können wir dies mit den obigen Kurven vergleichen, wobei wir ausschließlich WN (Breite des NMOS im Schalter) abstufen. Nach ein paar Iterationen von WN in den Simulationen ist klar, dass wir WN = 1170 µm benötigen, um das erforderlichen ΔRON zu erhalten, also weitaus mehr als die anfängliche Schätzung. Abbildung 5 zeigt unsere aktuellen Ergebnisse.
Während der RON des NMOS die richtige Empfindlichkeit gegenüber der Versorgungsspannung aufweist, haben die Kurven bei null Volt einen zu niedrigen Wert, und wir müssen den festgelegten Wert für RDN erhöhen. Nach Erhöhung und Iteration von RDN erhalten wir einen besten Wert von RDN = 22 Ω, und die resultierenden Kurven sind in Abbildung 6 dargestellt.
Abbildung 5. Simulationsergebnisse für den On-Widerstand mit festgelegtem WN.
Wir müssen hier mit zwei Variablen jonglieren, was zu mühsam ist. Es ist festzustellen, dass sich der RON-Wert mit der Versorgungsspannung ändert, weil der NMOS variabel angereichert wird, der RD-Wert sich jedoch nicht mit der Versorgungsspannung ändert (okay, bei Drains mit Drift-Regionen tut er dies wahrscheinlich doch, aber wir wollen es hier einfach halten).
Wenn wir den Unterschied für RON im Datenblatt zwischen den Versorgungsspannungen 10 V und 30 V beachten (11,4 Ω), können wir dies mit den obigen Kurven vergleichen, wobei wir ausschließlich WN (Breite des NMOS im Schalter) abstufen. Nach ein paar Iterationen von WN in den Simulationen ist klar, dass wir WN = 1170 µm benötigen, um das erforderlichen ΔRON zu erhalten, also weitaus mehr als die anfängliche Schätzung. Abbildung 5 zeigt unsere aktuellen Ergebnisse.
Während der RON des NMOS die richtige Empfindlichkeit gegenüber der Versorgungsspannung aufweist, haben die Kurven bei null Volt einen zu niedrigen Wert, und wir müssen den festgelegten Wert für RDN erhöhen. Nach Erhöhung und Iteration von RDN erhalten wir einen besten Wert von RDN = 22 Ω, und die resultierenden Kurven sind in Abbildung 6 dargestellt.
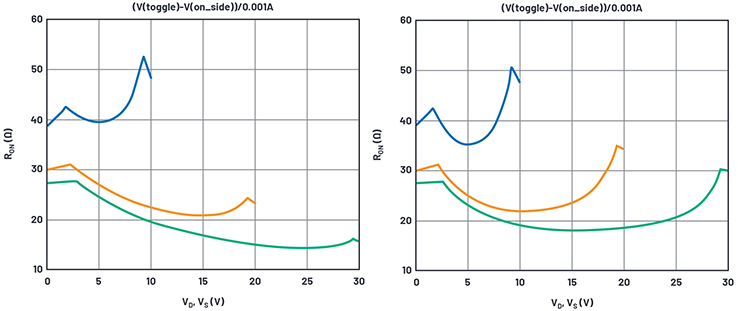 Abbildung 6. Simulationsergebnisse für den On-Widerstand mit festgelegtem RDN. / Abbildung 7. Simulationsergebnisse für den On-Widerstand mit festgelegtem WP und RDP.
Als Nächstes bestimmen wir WP (die Breite des PMOS im Schalter), um RON bei maximaler Spannung zu simulieren, und erhalten WP = 1700 µm, wiederum eine ganze Menge mehr als anfänglich vermutet. Mit einem ebenfalls auf 22 Ω festgelegten RDP erhalten wir die endgültige RON-Kurve in Abbildung 7.
Hier sehen wir eine ziemlich gute Übereinstimmung; es gibt nur einige wenige Merkmale, die sich vom Datenblatt unterscheiden. Zum einen sind die Wendepunkte in der Datenblattkurve glatt, während sie in der Simulation wirklich spitz sind. Dies liegt wahrscheinlich daran, dass das verwendete einfache MOS-Modell keine Unterschwelleneffekte unterstützt und das simulierte Bauelement sich bei VTO wirklich abschaltet. Reale Bauelemente sind bei VTO nicht ausgeschaltet, sondern verringern den Strom allmählich unterhalb dieser Spannung.
Ein weiterer Fehler ist in der 30-V-Kurve am deutlichsten zu erkennen. Der RON ist in der Mitte der Versorgungsspannung gegenüber dem Datenblatt um 15 % niedriger. Möglicherweise ist dies auf die ebenfalls nicht modellierten JFET-Effekte innerhalb der Drain-Drift-Region zurückzuführen.
Was die Temperatur betrifft, so gibt es eine gewisse, aber nicht allzu starke Übereinstimmung, wie in Abbildung 8 zu sehen ist.
Abbildung 6. Simulationsergebnisse für den On-Widerstand mit festgelegtem RDN. / Abbildung 7. Simulationsergebnisse für den On-Widerstand mit festgelegtem WP und RDP.
Als Nächstes bestimmen wir WP (die Breite des PMOS im Schalter), um RON bei maximaler Spannung zu simulieren, und erhalten WP = 1700 µm, wiederum eine ganze Menge mehr als anfänglich vermutet. Mit einem ebenfalls auf 22 Ω festgelegten RDP erhalten wir die endgültige RON-Kurve in Abbildung 7.
Hier sehen wir eine ziemlich gute Übereinstimmung; es gibt nur einige wenige Merkmale, die sich vom Datenblatt unterscheiden. Zum einen sind die Wendepunkte in der Datenblattkurve glatt, während sie in der Simulation wirklich spitz sind. Dies liegt wahrscheinlich daran, dass das verwendete einfache MOS-Modell keine Unterschwelleneffekte unterstützt und das simulierte Bauelement sich bei VTO wirklich abschaltet. Reale Bauelemente sind bei VTO nicht ausgeschaltet, sondern verringern den Strom allmählich unterhalb dieser Spannung.
Ein weiterer Fehler ist in der 30-V-Kurve am deutlichsten zu erkennen. Der RON ist in der Mitte der Versorgungsspannung gegenüber dem Datenblatt um 15 % niedriger. Möglicherweise ist dies auf die ebenfalls nicht modellierten JFET-Effekte innerhalb der Drain-Drift-Region zurückzuführen.
Was die Temperatur betrifft, so gibt es eine gewisse, aber nicht allzu starke Übereinstimmung, wie in Abbildung 8 zu sehen ist.
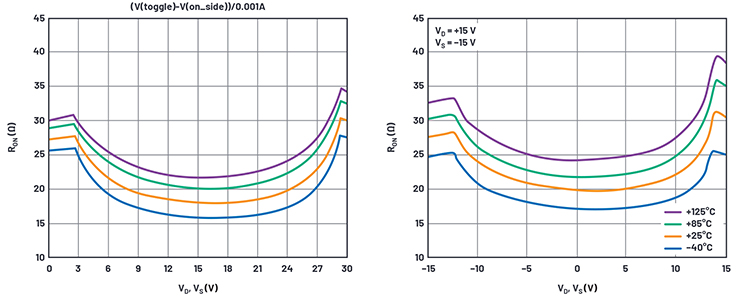 Abbildung 8. Ergebnisse aus Simulation und Datenblatt für RON über die Temperatur.
Die Simulation zeigt eine Temperaturabhängigkeit, die allerdings nicht so stark ist wie die in den Datenblattkurven. Im Simulationsmodell haben die RD-Terme keine Temperaturkoeffizienten. Die RDs könnten durch externe Widerstände mit korrekten Temperaturkoeffizienten modelliert werden, der Einfachheit halber belassen wir es aber dabei.
Gewinnung der LTspice-Modellparameter für die Ladungsinjektion
Wenn MOS-Transistoren abschalten, muss die Ladung im Kanal irgendwo hingehen, so dass sie aus den Drain- und Source-Anschlüssen austritt. Wenn ein Analogschalter ausgeschaltet wird, tritt auch Ladung aus, was als Ladungsinjektion bezeichnet wird. Eine gebräuchliche Art, diese zu messen, besteht darin, an einem Ende eines Einschalters eine feste Spannung und am anderen Ende einen großen Kondensator anzulegen.
Abbildung 8. Ergebnisse aus Simulation und Datenblatt für RON über die Temperatur.
Die Simulation zeigt eine Temperaturabhängigkeit, die allerdings nicht so stark ist wie die in den Datenblattkurven. Im Simulationsmodell haben die RD-Terme keine Temperaturkoeffizienten. Die RDs könnten durch externe Widerstände mit korrekten Temperaturkoeffizienten modelliert werden, der Einfachheit halber belassen wir es aber dabei.
Gewinnung der LTspice-Modellparameter für die Ladungsinjektion
Wenn MOS-Transistoren abschalten, muss die Ladung im Kanal irgendwo hingehen, so dass sie aus den Drain- und Source-Anschlüssen austritt. Wenn ein Analogschalter ausgeschaltet wird, tritt auch Ladung aus, was als Ladungsinjektion bezeichnet wird. Eine gebräuchliche Art, diese zu messen, besteht darin, an einem Ende eines Einschalters eine feste Spannung und am anderen Ende einen großen Kondensator anzulegen.
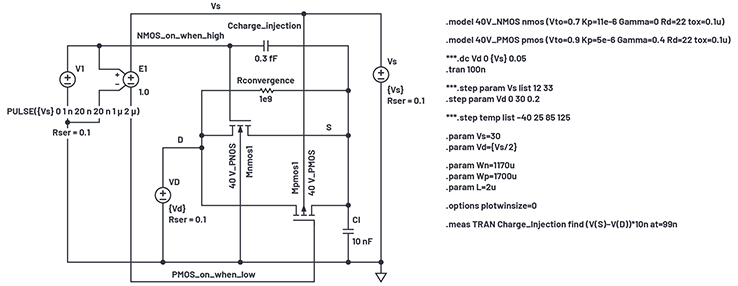 Abbildung 9. Simulationsaufbau für die Ladungsinjektion.
Beim Ausschalten wird die Ladung vom Kondensator aufgefangen und ein kleiner Spannungssprung entsteht. Wir fügen nun die Gate-Oxiddicke TOX = 1 × 10-7 zu den MOS-Modellen hinzu (die Gate-Kapazität ist die größte Quelle der Ladungsinjektion). Unser Simulationsaufbau ist in Abbildung 9 dargestellt.
Abbildung 9. Simulationsaufbau für die Ladungsinjektion.
Beim Ausschalten wird die Ladung vom Kondensator aufgefangen und ein kleiner Spannungssprung entsteht. Wir fügen nun die Gate-Oxiddicke TOX = 1 × 10-7 zu den MOS-Modellen hinzu (die Gate-Kapazität ist die größte Quelle der Ladungsinjektion). Unser Simulationsaufbau ist in Abbildung 9 dargestellt.
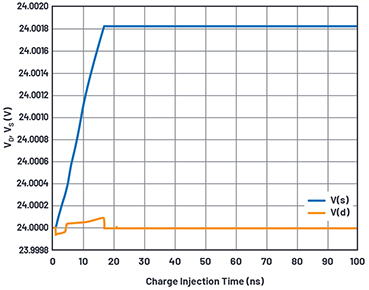 Abbildung 10. Wellenformen bei der Simulation der Ladungsinjektion.
Bei der Testschaltung für die Ladungsinjektion im Datenblatt wird eine Spannungsquelle am Anschluss D und ein Kondensator Cl am Anschluss S des Schalters platziert. Wenn die Schalttransistoren abgeschaltet werden, wird Cl isoliert und nimmt die von den Schaltern zugeführte Ladung auf. Die Wellenform eines solchen Ereignisses mit auf 24 V gehaltener Spannung VD bei einer 30-V-Versorgung ist in Abbildung 10 dargestellt.
Die injizierte Ladung entspricht dem Spannungssprung zwischen V(S) und V(D) multipliziert mit dem 10 nF-Haltekondensator. Wir können die Schaltspannung VD über die Versorgungsspannung stufenweise erhöhen und die meas-Anweisung verwenden, um den Wert der Ladungsinjektion bei jeder Spannung zu erfassen. Abbildung 11 zeigt die Datenblattkurve und die simulierten Ergebnisse.
Abbildung 10. Wellenformen bei der Simulation der Ladungsinjektion.
Bei der Testschaltung für die Ladungsinjektion im Datenblatt wird eine Spannungsquelle am Anschluss D und ein Kondensator Cl am Anschluss S des Schalters platziert. Wenn die Schalttransistoren abgeschaltet werden, wird Cl isoliert und nimmt die von den Schaltern zugeführte Ladung auf. Die Wellenform eines solchen Ereignisses mit auf 24 V gehaltener Spannung VD bei einer 30-V-Versorgung ist in Abbildung 10 dargestellt.
Die injizierte Ladung entspricht dem Spannungssprung zwischen V(S) und V(D) multipliziert mit dem 10 nF-Haltekondensator. Wir können die Schaltspannung VD über die Versorgungsspannung stufenweise erhöhen und die meas-Anweisung verwenden, um den Wert der Ladungsinjektion bei jeder Spannung zu erfassen. Abbildung 11 zeigt die Datenblattkurve und die simulierten Ergebnisse.
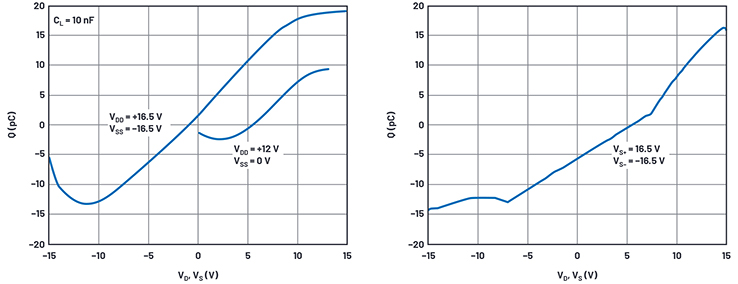 Abbildung 11. Wellenformen für die Ladungsinjektion aus Datenblatt und Simulation
Unser einfaches MOS-Modell bildet die Form der Datenblattkurve nicht sehr gut nach, aber die Spitze-Spitze-Ladungsinjektion beträgt 32 pC in den Datenblattkurven und 31 pC in der Simulation. Dies ist schon überraschend nahe dran, aber wenn es sein müsste, könnten wir noch TOX optimieren, um die Simulationsergebnisse zu perfektionieren.
Es besteht ein Versatz zwischen den Kurven, den wir mit CCHARGE_INJECTION ausgleichen können. Nach Herumspielen mit einigen Werten wählen wir als optimalen Wert CCHARGE_INJECTION = 0,28 pF. Wenn eine Verschiebung mit entgegengesetzter Polarität erforderlich wäre, würde CCHARGE_INJECTION wieder mit dem Knoten PMOS_on_when_low verbunden werden.
Der Anpassungskondensator CCHARGE_INJECTION war eine bequeme Möglichkeit, die Ladungsinjektion gegenüber der Simulationskurve der analogen Spannung auszugleichen. Was wäre, wenn die simulierte Spitze-Spitze-Injektion zu klein wäre? Nun, der größte Teil der Ladungsinjektion besteht zumeist aus den Schwankungen der Gatespannung der Schalter, welche Ladung durch die Gatekanal-Kapazität der Schalttransistoren schicken. Wenn wir eine zu geringe Injektion simulieren, können wir einfach einen oder beide Gate-Bereiche vergrößern. Dazu müssten wir die Parameter L und W eines Schaltgerätes um den gleichen Faktor erhöhen, wobei darauf zu achten ist, dass das Verhältnis W/L-Verhältnis, das den On-Widerstand festlegt, nicht verändert wird. Anstatt CCHARGE_INJECTION zu verwenden, hätten wir die auch die Werte W und L des NMOS erhöhen können.
Alternativ könnten wir den Wert für TOX in jedem Bauteil anpassen, um eine bessere Korrelation der Ladungsinjektion zu erhalten. Das wäre physikalisch nicht möglich – aber es ist ja auch nur eine Simulation. Bei den einfachen Modellen, die wir verwenden, beeinflusst TOX andere Schaltungsverhalten nicht.
Bestimmung von LTspice-Modell-Parametern für Kapazitäten
Nachdem wir die Parameter für gute Simulationsergebnisse für RON und Ladungsinjektion eingestellt haben, simulieren wir nun die Kapazitäten der Anschlüsse S und D.
Ein wichtiger Punkt ist, dass sowohl der Drain- als auch der Source-Bereich von Hochspannungs-MOS-Schaltern Driftbereiche aufweisen müssen. Als Schalter kann man den funktionellen Unterschied zwischen Source- und Drain-Anschlüssen nicht erkennen, und das Substrat- Potenzial gegenüber den Drain und Source-Anschlüssen erfordert die entsprechenden Driftregionen in beiden. Dies gilt auch für die Soft-Diffusionen im mittleren Spannungsbereich, die jedoch bei Kleinspannungs-MOS nicht vorhanden sind. Wir haben den verteilten Widerstand in der Driftregion, der sowohl im Drain als auch in der Source vorhanden wäre, in RD zusammengefasst, was bei Schaltern gut funktioniert, jedoch nicht bei Transistoren in der Sättigung.
Abbildung 12 zeigt unseren Simulationsaufbau.
Abbildung 11. Wellenformen für die Ladungsinjektion aus Datenblatt und Simulation
Unser einfaches MOS-Modell bildet die Form der Datenblattkurve nicht sehr gut nach, aber die Spitze-Spitze-Ladungsinjektion beträgt 32 pC in den Datenblattkurven und 31 pC in der Simulation. Dies ist schon überraschend nahe dran, aber wenn es sein müsste, könnten wir noch TOX optimieren, um die Simulationsergebnisse zu perfektionieren.
Es besteht ein Versatz zwischen den Kurven, den wir mit CCHARGE_INJECTION ausgleichen können. Nach Herumspielen mit einigen Werten wählen wir als optimalen Wert CCHARGE_INJECTION = 0,28 pF. Wenn eine Verschiebung mit entgegengesetzter Polarität erforderlich wäre, würde CCHARGE_INJECTION wieder mit dem Knoten PMOS_on_when_low verbunden werden.
Der Anpassungskondensator CCHARGE_INJECTION war eine bequeme Möglichkeit, die Ladungsinjektion gegenüber der Simulationskurve der analogen Spannung auszugleichen. Was wäre, wenn die simulierte Spitze-Spitze-Injektion zu klein wäre? Nun, der größte Teil der Ladungsinjektion besteht zumeist aus den Schwankungen der Gatespannung der Schalter, welche Ladung durch die Gatekanal-Kapazität der Schalttransistoren schicken. Wenn wir eine zu geringe Injektion simulieren, können wir einfach einen oder beide Gate-Bereiche vergrößern. Dazu müssten wir die Parameter L und W eines Schaltgerätes um den gleichen Faktor erhöhen, wobei darauf zu achten ist, dass das Verhältnis W/L-Verhältnis, das den On-Widerstand festlegt, nicht verändert wird. Anstatt CCHARGE_INJECTION zu verwenden, hätten wir die auch die Werte W und L des NMOS erhöhen können.
Alternativ könnten wir den Wert für TOX in jedem Bauteil anpassen, um eine bessere Korrelation der Ladungsinjektion zu erhalten. Das wäre physikalisch nicht möglich – aber es ist ja auch nur eine Simulation. Bei den einfachen Modellen, die wir verwenden, beeinflusst TOX andere Schaltungsverhalten nicht.
Bestimmung von LTspice-Modell-Parametern für Kapazitäten
Nachdem wir die Parameter für gute Simulationsergebnisse für RON und Ladungsinjektion eingestellt haben, simulieren wir nun die Kapazitäten der Anschlüsse S und D.
Ein wichtiger Punkt ist, dass sowohl der Drain- als auch der Source-Bereich von Hochspannungs-MOS-Schaltern Driftbereiche aufweisen müssen. Als Schalter kann man den funktionellen Unterschied zwischen Source- und Drain-Anschlüssen nicht erkennen, und das Substrat- Potenzial gegenüber den Drain und Source-Anschlüssen erfordert die entsprechenden Driftregionen in beiden. Dies gilt auch für die Soft-Diffusionen im mittleren Spannungsbereich, die jedoch bei Kleinspannungs-MOS nicht vorhanden sind. Wir haben den verteilten Widerstand in der Driftregion, der sowohl im Drain als auch in der Source vorhanden wäre, in RD zusammengefasst, was bei Schaltern gut funktioniert, jedoch nicht bei Transistoren in der Sättigung.
Abbildung 12 zeigt unseren Simulationsaufbau.
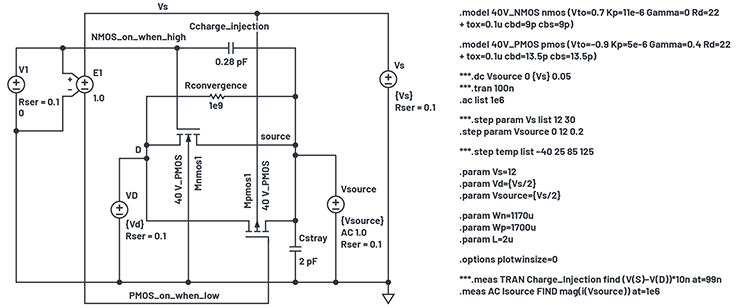 Abbildung 12. Simulationsaufbau für die Ermittlung der Off-Kapazität
In LTspice kann man eine .ac-Analyse nur auf einer Frequenz ausführen, indem man die Listenoption in .ac verwendet, dabei aber nur ein Frequenzargument angibtn (hier 1 MHz). Anschließend lässt man eine .step VSOURCE-Gleichspannung über den Versorgungsspannungsbereich laufen, um einen Verlauf der Kapazität gegenüber der Spannung zu erhalten.
Der D-Anschluss des Ausschalters wird auf mittlerer Versorgungsspannung gehalten. Der S-Anschluss, der hier zur Vermeidung von Verwechslungen mit VS in Source umbenannt wurde, wird von einer Gleichspannungsquelle, die 0 V bis VS überstreicht, mit einer Wechselspannungsansteuerung von 1 V angesteuert. Die Kapazität wird von I(VSOURCE)/(2 × π × 1 MHz × 1 V) abgeleitet. Die Logikansteuerung V1 wird auf 0 V geändert, um die Transistoren auszuschalten.
Die Drain- und Source-Kapazitäten zum Substrat (Bulk) werden in der Modellerklärung als CBD bzw. CBS bezeichnet.
Das Modell verfügt über eingebaute Standardkonzentrationen, eine interne Spannung und einen Exponenten, die die Spannungen über CBD und CBS variabel machen. Da diese symmetrisch sind, würden die Drain- und Source-Kapazitäten gleich gesetzt werden. Da der PMOS eine andere Breite als der NMOS hat, ist darüber hinaus das Verhältnis von CBD,NMOS/CBD,PMOS = CBS,NMOS/CBS,PMOS = WN/WP, welches wir bei der Modellierung des On-Widerstands ermittelt haben. Abbildung 13 zeigt die Simulationsergebnisse.
Abbildung 12. Simulationsaufbau für die Ermittlung der Off-Kapazität
In LTspice kann man eine .ac-Analyse nur auf einer Frequenz ausführen, indem man die Listenoption in .ac verwendet, dabei aber nur ein Frequenzargument angibtn (hier 1 MHz). Anschließend lässt man eine .step VSOURCE-Gleichspannung über den Versorgungsspannungsbereich laufen, um einen Verlauf der Kapazität gegenüber der Spannung zu erhalten.
Der D-Anschluss des Ausschalters wird auf mittlerer Versorgungsspannung gehalten. Der S-Anschluss, der hier zur Vermeidung von Verwechslungen mit VS in Source umbenannt wurde, wird von einer Gleichspannungsquelle, die 0 V bis VS überstreicht, mit einer Wechselspannungsansteuerung von 1 V angesteuert. Die Kapazität wird von I(VSOURCE)/(2 × π × 1 MHz × 1 V) abgeleitet. Die Logikansteuerung V1 wird auf 0 V geändert, um die Transistoren auszuschalten.
Die Drain- und Source-Kapazitäten zum Substrat (Bulk) werden in der Modellerklärung als CBD bzw. CBS bezeichnet.
Das Modell verfügt über eingebaute Standardkonzentrationen, eine interne Spannung und einen Exponenten, die die Spannungen über CBD und CBS variabel machen. Da diese symmetrisch sind, würden die Drain- und Source-Kapazitäten gleich gesetzt werden. Da der PMOS eine andere Breite als der NMOS hat, ist darüber hinaus das Verhältnis von CBD,NMOS/CBD,PMOS = CBS,NMOS/CBS,PMOS = WN/WP, welches wir bei der Modellierung des On-Widerstands ermittelt haben. Abbildung 13 zeigt die Simulationsergebnisse.
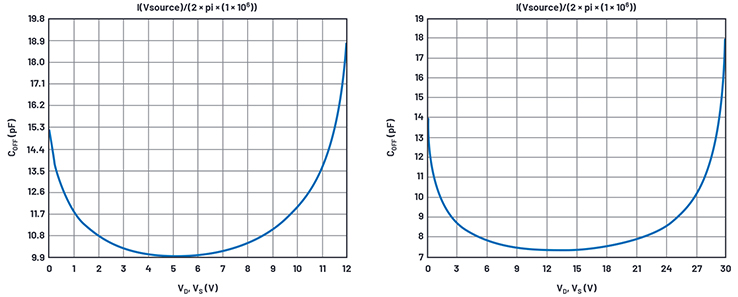 Abbildung 13. Ergebnisse für die Off-Kapazität in Abhängigkeit von der Gleichspannung bei VS = 12 V (links) und 30 V (rechts).
Angezeigt wird I(VSOURCE)/(2 × π × 1 MHz), was eine Kapazität darstellt. LTspice weiß dies allerdings nicht und zeigt pA statt pF an.
Leider haben wir keine Datenblattkurven zum Vergleich zur Verfügung. Aus der Spezifikationstabelle im Datenblatt wissen wir, dass die Kapazität - wahrscheinlich in der Mitte der Versorgungsspannungen, jedoch nicht im Datenblatt angegeben - typischerweise 7 pF bei Versorgung mit 30 V und 12 pF bei Versorgung mit 12 V beträgt. Ich habe die CBs angepasst, um die 7 pF-Kurve bei 30 V zu erhalten, aber nur 10 pF bei einer 12-V-Versorgung simuliert. Nach Herumspielen mit den internen Potenzial- und Kapazitätsformel-Exponenten lässt das verwendete Modell keine Flexibilität zur Verbesserung der 12 V/30 V-Übereinstimmung zu.
Abbildung 14 zeigt den Simulationsaufbau für die Off-State-Kapazität.
Abbildung 13. Ergebnisse für die Off-Kapazität in Abhängigkeit von der Gleichspannung bei VS = 12 V (links) und 30 V (rechts).
Angezeigt wird I(VSOURCE)/(2 × π × 1 MHz), was eine Kapazität darstellt. LTspice weiß dies allerdings nicht und zeigt pA statt pF an.
Leider haben wir keine Datenblattkurven zum Vergleich zur Verfügung. Aus der Spezifikationstabelle im Datenblatt wissen wir, dass die Kapazität - wahrscheinlich in der Mitte der Versorgungsspannungen, jedoch nicht im Datenblatt angegeben - typischerweise 7 pF bei Versorgung mit 30 V und 12 pF bei Versorgung mit 12 V beträgt. Ich habe die CBs angepasst, um die 7 pF-Kurve bei 30 V zu erhalten, aber nur 10 pF bei einer 12-V-Versorgung simuliert. Nach Herumspielen mit den internen Potenzial- und Kapazitätsformel-Exponenten lässt das verwendete Modell keine Flexibilität zur Verbesserung der 12 V/30 V-Übereinstimmung zu.
Abbildung 14 zeigt den Simulationsaufbau für die Off-State-Kapazität.
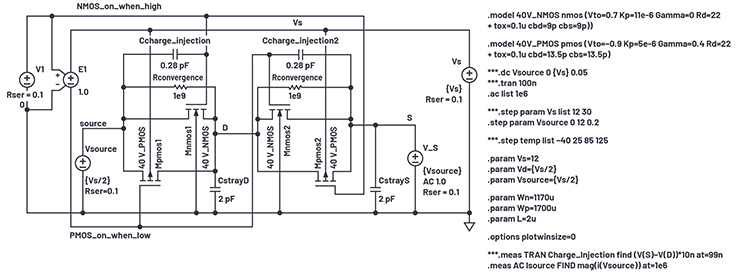 Abbildung 14. Simulationsaufbau für die Off-State-Kapazität.
Hier ist der rechte Schalter eines vollen spdt-Schalters eingeschaltet, während der linke Schalter ausgeschaltet und an eine VS/2-Quelle angeschlossen ist. Die Kapazitäten der rechten Hälfte des linken Schalters und die vollen Kapazitäten des rechten Schalters sowie die unvermeidlichen parasitären Kapazitäten an den Anschlüssen D und S werden alle parallel geschaltet und von unserem 1-MHz-Testsignal an der Vs-Quelle angesteuert, deren Gleichspannungspegel von Masse bis VS gestuft ist. Abbildung 15 zeigt die Ergebnisse.
Abbildung 14. Simulationsaufbau für die Off-State-Kapazität.
Hier ist der rechte Schalter eines vollen spdt-Schalters eingeschaltet, während der linke Schalter ausgeschaltet und an eine VS/2-Quelle angeschlossen ist. Die Kapazitäten der rechten Hälfte des linken Schalters und die vollen Kapazitäten des rechten Schalters sowie die unvermeidlichen parasitären Kapazitäten an den Anschlüssen D und S werden alle parallel geschaltet und von unserem 1-MHz-Testsignal an der Vs-Quelle angesteuert, deren Gleichspannungspegel von Masse bis VS gestuft ist. Abbildung 15 zeigt die Ergebnisse.
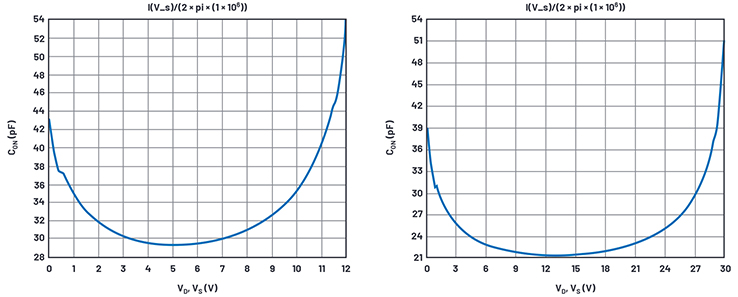 Abbildung 15. Simulationsergebnisse On-Kapazität vs. Gleichspannung bei VS = 12 V (links) und 30 V (rechts).
Die Simulation ergibt 29,5 pF bzw. 21,4 pF, während im Datenblatt 26 pF bzw. 25 pF angegeben sind. Angesichts der üblichen Kapazitätsschwankungen von Leiterplatten-Layouts können wir dies als nahe genug betrachten.
Leckströme
Die Datenblattkurven zeigen bei 25 °C spannungsabhängige Leckströme im pA-Bereich, während die Datenblattspezifikation lediglich Leckströme im Bereich von einigen hundert pA garantiert. Ich bin mehr von den Ergebnissen der Kurven bei 25 °C beeindruckt. Die geringen Leckströme wurden bei diesem Gerät offenbar nicht für wichtig genug gehalten, um sie beim Test zu garantieren. Fairerweise muss man sagen, dass die Messung einzelner pA einen hohen technischen Entwicklungsaufwand und lange Testzeiten erfordert.
Bei 85 °C werden einige nA garantiert (die effizient gemessen werden können) mit einem typischen Ergebnis im Bereich von einigen hundert pA. Ich werde diese typischen Ergebnisse als gut akzeptieren.
Abbildung 15. Simulationsergebnisse On-Kapazität vs. Gleichspannung bei VS = 12 V (links) und 30 V (rechts).
Die Simulation ergibt 29,5 pF bzw. 21,4 pF, während im Datenblatt 26 pF bzw. 25 pF angegeben sind. Angesichts der üblichen Kapazitätsschwankungen von Leiterplatten-Layouts können wir dies als nahe genug betrachten.
Leckströme
Die Datenblattkurven zeigen bei 25 °C spannungsabhängige Leckströme im pA-Bereich, während die Datenblattspezifikation lediglich Leckströme im Bereich von einigen hundert pA garantiert. Ich bin mehr von den Ergebnissen der Kurven bei 25 °C beeindruckt. Die geringen Leckströme wurden bei diesem Gerät offenbar nicht für wichtig genug gehalten, um sie beim Test zu garantieren. Fairerweise muss man sagen, dass die Messung einzelner pA einen hohen technischen Entwicklungsaufwand und lange Testzeiten erfordert.
Bei 85 °C werden einige nA garantiert (die effizient gemessen werden können) mit einem typischen Ergebnis im Bereich von einigen hundert pA. Ich werde diese typischen Ergebnisse als gut akzeptieren.
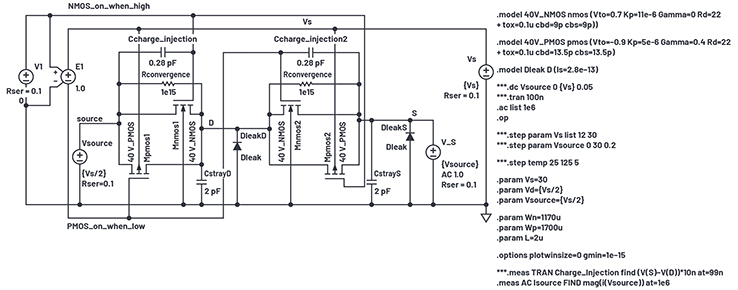 Abbildung 16. Simulationsaufbau zur Ermittlung der Leckströme
Die Leckströme sind ein Produktmangel; es gibt diesbezüglich keine genauen Statistiken und sie schwanken stark mit der Temperatur. Es ist nicht die Art von Vorgabe, nach der wir unseren Entwurf ausrichten - vielmehr ist es eine Größe, die die Schaltkreise stört, mit denen der Schalter verbunden ist. Bei der Verwendung von Makromodellen werden sämtliche Leckströme von signifikanter Größe als Schaltungsdefekte simuliert, was eine nützliche Warnung für den Entwickler darstellt. Ich wähle einen Zielwert von 1 nA für einen Schließer bei 85 °C.
Abbildung 16. Simulationsaufbau zur Ermittlung der Leckströme
Die Leckströme sind ein Produktmangel; es gibt diesbezüglich keine genauen Statistiken und sie schwanken stark mit der Temperatur. Es ist nicht die Art von Vorgabe, nach der wir unseren Entwurf ausrichten - vielmehr ist es eine Größe, die die Schaltkreise stört, mit denen der Schalter verbunden ist. Bei der Verwendung von Makromodellen werden sämtliche Leckströme von signifikanter Größe als Schaltungsdefekte simuliert, was eine nützliche Warnung für den Entwickler darstellt. Ich wähle einen Zielwert von 1 nA für einen Schließer bei 85 °C.
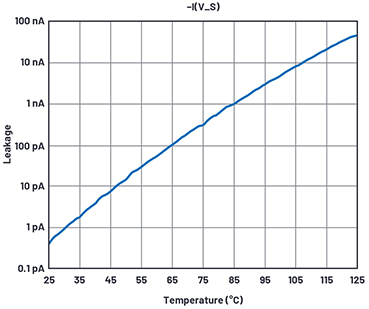 Abbildung 17. Simulationsergebnisse der Leckströme über die Temperatur
Das Modell, das wir hier haben, zeigt keine Leckströme jenseits der Ströme über RCONVERGENCE und GMIN. GMIN ist ein Widerstand, den der Simulator überVerbindungen platziert, um die Konvergenz zu erleichtern. Normalerweise hat dieser einen Leitwert von 1 × 10-12, aber bei Versorgungsspannungen von 30 V können wir ein Vielfaches der Ströme von 30 pA erhalten, was für diese Aufgabe viel zu hoch ist. GMIN wird in daher der Zeile .options der Simulation auf 1 × 10-15 verringert und RCONVERGENCE auf 1 × 1015 erhöht.
Der physikalische Ursprung dieser Leckströme sind vermutlich größtenteils die an jedem Pin angeschlossenen Schutzdioden gegen elektrostatische Entladung (ESD). Wir setzen diese in den Simulationsaufbau in Abbildung 16 ein.'
Nach dem Hantieren mit IS im Diodenmodell erhalten wir die Leckströme über die Temperatur in Abbildung 17.
Logik-Schnittstelle und Gate-Treiber
Eine rein verhaltensbasierte Logic-to-Gate-Treiberschaltung ist in Abbildung 18 dargestellt.
Abbildung 17. Simulationsergebnisse der Leckströme über die Temperatur
Das Modell, das wir hier haben, zeigt keine Leckströme jenseits der Ströme über RCONVERGENCE und GMIN. GMIN ist ein Widerstand, den der Simulator überVerbindungen platziert, um die Konvergenz zu erleichtern. Normalerweise hat dieser einen Leitwert von 1 × 10-12, aber bei Versorgungsspannungen von 30 V können wir ein Vielfaches der Ströme von 30 pA erhalten, was für diese Aufgabe viel zu hoch ist. GMIN wird in daher der Zeile .options der Simulation auf 1 × 10-15 verringert und RCONVERGENCE auf 1 × 1015 erhöht.
Der physikalische Ursprung dieser Leckströme sind vermutlich größtenteils die an jedem Pin angeschlossenen Schutzdioden gegen elektrostatische Entladung (ESD). Wir setzen diese in den Simulationsaufbau in Abbildung 16 ein.'
Nach dem Hantieren mit IS im Diodenmodell erhalten wir die Leckströme über die Temperatur in Abbildung 17.
Logik-Schnittstelle und Gate-Treiber
Eine rein verhaltensbasierte Logic-to-Gate-Treiberschaltung ist in Abbildung 18 dargestellt.
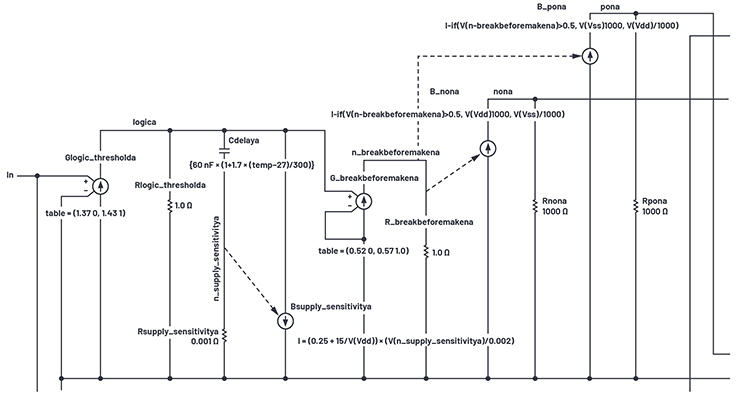 Abbildung 18. Verhaltensbasierte Logic-to-Gate-Schnittstelle
Der externe Logikeingang befindet sich am In-Anschluss links in Abbildung 18. Es ist der Eingang einer idealen Transkonduktanz Glogic_thresholda, die eine stückweise lineare Übertragungsfunktion hat. Bei Logikeingängen unter 1,37 V beträgt der Ausgang am Logikknoten 0 V; bei Eingängen über 1,43 V liegt logica bei 1 V; und zwischen 1,37 V und 1,43 V bewegt sich logica linear von 0 V auf 1 . Glogic_thresholda ignoriert also Versorgungsspannungsschwankungen, um eine Eingangsschwellenspannung von 1,4 V bereitzustellen.
Cdelaya verlangsamt kurzzeitig den Knoten logica, so dass wir einige Zeitpunkte aus diesem herausgreifen können. Um einen Komparator zu erzeugen, verwenden wir wieder eine Transkonduktanz, hier Gbreakbeforemakena, deren Ausgang wieder von 0 V auf 1 V geht, jedoch mit einem etwas über 0,5 V verschobenen Schwellenwert. Wie in Abbildung 19 zu sehen ist, ermöglichen die verschobenen Abgriffsspannungen 0,52 V und 0,57 V anstelle von 0,5 V ein schnelleres Abschalten von Exponenten, die von 1 V abfallen, als die Einschaltzeit für Exponenten, die von 0 V ansteigen.
Abbildung 18. Verhaltensbasierte Logic-to-Gate-Schnittstelle
Der externe Logikeingang befindet sich am In-Anschluss links in Abbildung 18. Es ist der Eingang einer idealen Transkonduktanz Glogic_thresholda, die eine stückweise lineare Übertragungsfunktion hat. Bei Logikeingängen unter 1,37 V beträgt der Ausgang am Logikknoten 0 V; bei Eingängen über 1,43 V liegt logica bei 1 V; und zwischen 1,37 V und 1,43 V bewegt sich logica linear von 0 V auf 1 . Glogic_thresholda ignoriert also Versorgungsspannungsschwankungen, um eine Eingangsschwellenspannung von 1,4 V bereitzustellen.
Cdelaya verlangsamt kurzzeitig den Knoten logica, so dass wir einige Zeitpunkte aus diesem herausgreifen können. Um einen Komparator zu erzeugen, verwenden wir wieder eine Transkonduktanz, hier Gbreakbeforemakena, deren Ausgang wieder von 0 V auf 1 V geht, jedoch mit einem etwas über 0,5 V verschobenen Schwellenwert. Wie in Abbildung 19 zu sehen ist, ermöglichen die verschobenen Abgriffsspannungen 0,52 V und 0,57 V anstelle von 0,5 V ein schnelleres Abschalten von Exponenten, die von 1 V abfallen, als die Einschaltzeit für Exponenten, die von 0 V ansteigen.
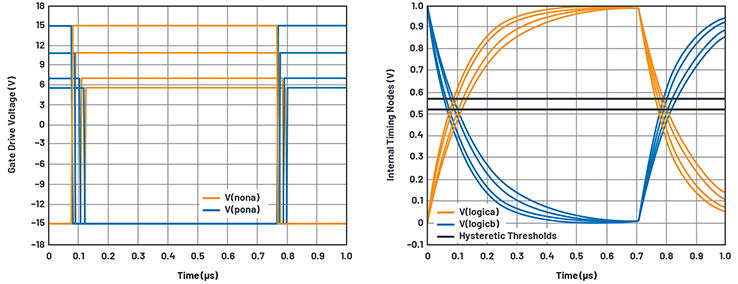 Abbildung 19. Break before Make-Zeitverhalten.
Die volle Gate-Treiberspannung wird von den Stromquellen mit B_non- und B_pon-Verhalten erzeugt. B_nona liefert einen Strom von VDD/1000, wenn der Knoten n_breakbeforemakena > 0,5 V ist, und treibt die Spannung am Knoten nona auf VDD, da durch einen 1000 Ω-Widerstand belastet.
Wenn der Knoten n_breakbeforemakena < 0,5 V ist, wird der Knoten nona auf VSS gebracht. Damit haben wir einen schönen Rail-to-Rail-Gate-Treiber, der mit den Versorgungsspannungen kompatibel ist und eine feste Eingangsschwelle von 1,4 V hat.
Es gibt noch eine weitere Eigenschaft, die einer Erklärung bedarf. Es ist zu beachten, dass in Abbildung 20 die Verzögerungszeiten durch höhere Versorgungsspannungen verkürzt werden.. Dies wird mittels B_supplysensitivitya implementiert, bei der eine Bruchteil ihres eigenen dynamischen Stroms, der in Abhängigkeit vom VDD variiert, an Cdelaya zurückgeführt wird. An Rsupply_sensitivitya fällt aufgrund des Cdelaya-Stroms nur sehr wenig Spannung ab, so dass sich Cdelaya im Grunde wie ein reiner Kondensator verhält . Das Einspeisen einer Kopie des Stroms von Cdelaya zurück zu Cdelaya erzeugt im Wesentlichen einen steuerbaren variablen Kondensator, und d mathematisch erzeugt Bsupply_sensitivitya die Kurve der Verzögerung in Abhängigkeit von VDD in Abbildung 20.
Abbildung 19. Break before Make-Zeitverhalten.
Die volle Gate-Treiberspannung wird von den Stromquellen mit B_non- und B_pon-Verhalten erzeugt. B_nona liefert einen Strom von VDD/1000, wenn der Knoten n_breakbeforemakena > 0,5 V ist, und treibt die Spannung am Knoten nona auf VDD, da durch einen 1000 Ω-Widerstand belastet.
Wenn der Knoten n_breakbeforemakena < 0,5 V ist, wird der Knoten nona auf VSS gebracht. Damit haben wir einen schönen Rail-to-Rail-Gate-Treiber, der mit den Versorgungsspannungen kompatibel ist und eine feste Eingangsschwelle von 1,4 V hat.
Es gibt noch eine weitere Eigenschaft, die einer Erklärung bedarf. Es ist zu beachten, dass in Abbildung 20 die Verzögerungszeiten durch höhere Versorgungsspannungen verkürzt werden.. Dies wird mittels B_supplysensitivitya implementiert, bei der eine Bruchteil ihres eigenen dynamischen Stroms, der in Abhängigkeit vom VDD variiert, an Cdelaya zurückgeführt wird. An Rsupply_sensitivitya fällt aufgrund des Cdelaya-Stroms nur sehr wenig Spannung ab, so dass sich Cdelaya im Grunde wie ein reiner Kondensator verhält . Das Einspeisen einer Kopie des Stroms von Cdelaya zurück zu Cdelaya erzeugt im Wesentlichen einen steuerbaren variablen Kondensator, und d mathematisch erzeugt Bsupply_sensitivitya die Kurve der Verzögerung in Abhängigkeit von VDD in Abbildung 20.
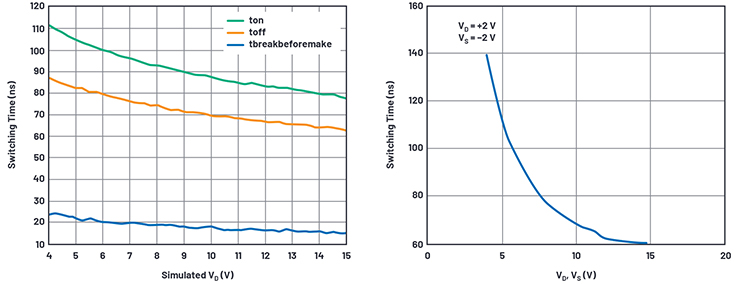 Abbildung 20. Ergebnisse für das Break-before-Make-Zeitverhalten aus Simulation und Datenblatt
Nun emuliert unsere Schaltung die TON-Verzögerung als 111 ns für VDD = 4, während die Datenblattkurve 140 ns angibt. Für VDD = 15 V beträgt die simulierte Verzögerung 77 ns gegenüber einer Verzögerung von 60 ns im Datenblatt. Dies ist keine besonders gute Korrelation; ich überlasse es dem Leser, die Funktion Bsupply_sensitivity zu verfeinern, um dies zu verbessern. Immerhin variiert der Break-before-Make-Zeit schön zwischen 15 ns und 24 ns.
Abbildung 20. Ergebnisse für das Break-before-Make-Zeitverhalten aus Simulation und Datenblatt
Nun emuliert unsere Schaltung die TON-Verzögerung als 111 ns für VDD = 4, während die Datenblattkurve 140 ns angibt. Für VDD = 15 V beträgt die simulierte Verzögerung 77 ns gegenüber einer Verzögerung von 60 ns im Datenblatt. Dies ist keine besonders gute Korrelation; ich überlasse es dem Leser, die Funktion Bsupply_sensitivity zu verfeinern, um dies zu verbessern. Immerhin variiert der Break-before-Make-Zeit schön zwischen 15 ns und 24 ns.
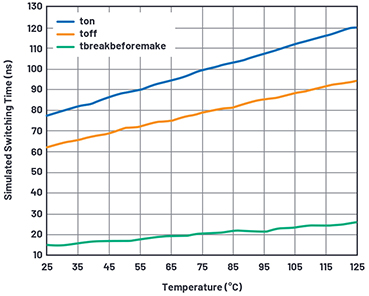 Abbildung 21. Zeitliche Verzögerungen in Abhängigkeit von der Temperatur.
Zwar haben wir nicht viele Datenblattdaten bezüglich der Verzögerung in Abhängigkeit von der Temperatur, aber ich habe einen Temperaturterm zu Cdelaya hinzugefügt, um zumindest die Verlangsamung des Modells im heißen Zustand zu ermöglichen, wie in Abbildung 21 zu sehen ist.
Zusammensetzen des Makromodells
Abbildung 22 zeigt den zusammengesetzten Analogschalter, der zu einem Teilschaltkreis (subcircuit) wird. Anstelle von Parametern wurden harte Zahlen für L und W in die Transistorsymbole eingefügt, und alle Erregungs- und E/A-Signale wurden zugunsten der Pin-Anschlüsse SA, D, SB, In, V , V und Gnd_pin entfernt.
Abbildung 21. Zeitliche Verzögerungen in Abhängigkeit von der Temperatur.
Zwar haben wir nicht viele Datenblattdaten bezüglich der Verzögerung in Abhängigkeit von der Temperatur, aber ich habe einen Temperaturterm zu Cdelaya hinzugefügt, um zumindest die Verlangsamung des Modells im heißen Zustand zu ermöglichen, wie in Abbildung 21 zu sehen ist.
Zusammensetzen des Makromodells
Abbildung 22 zeigt den zusammengesetzten Analogschalter, der zu einem Teilschaltkreis (subcircuit) wird. Anstelle von Parametern wurden harte Zahlen für L und W in die Transistorsymbole eingefügt, und alle Erregungs- und E/A-Signale wurden zugunsten der Pin-Anschlüsse SA, D, SB, In, V , V und Gnd_pin entfernt.
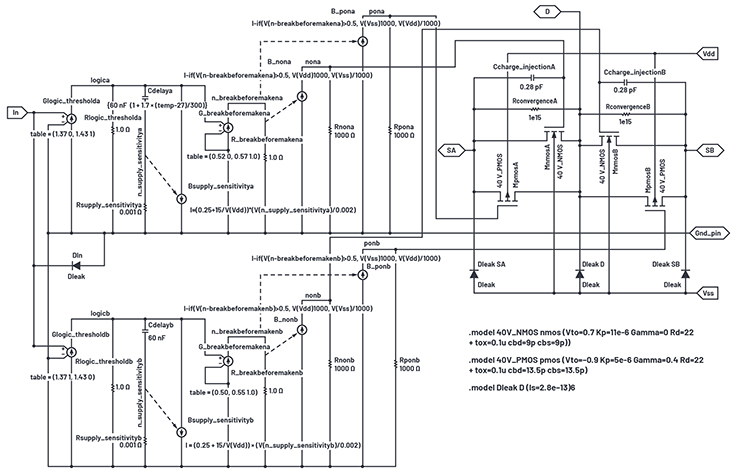 Abbildung 22. Zusammengesetzte SPDT-Teilschaltung spdt 40V.asc.
Eine zweite Logikschnittstelle ist für den anderen Schalter des spdt-Paars vorgesehen. ESD-Schutzdioden sind zwischen den analogen Anschlüssen und VSS sowie zwischen dem logischen Eingang und Masse installiert. Zu beachten ist, dass das Suffix „-a" in den Namen der oberen Bausteine und Knoten der Logikschnittstelle als Suffix „-b“ in der unteren Schnittstelle repliziert wird. Die Schnittstelle Glogic_thresholdb hat den entgegengesetzten Ausgang aus der Tabelle in Glogic_ thresholda, damit das eine oder andere Schalterpaar arbeiten kann, anstatt gleichzeitig eingeschaltet zu werden.
Abbildung 22. Zusammengesetzte SPDT-Teilschaltung spdt 40V.asc.
Eine zweite Logikschnittstelle ist für den anderen Schalter des spdt-Paars vorgesehen. ESD-Schutzdioden sind zwischen den analogen Anschlüssen und VSS sowie zwischen dem logischen Eingang und Masse installiert. Zu beachten ist, dass das Suffix „-a" in den Namen der oberen Bausteine und Knoten der Logikschnittstelle als Suffix „-b“ in der unteren Schnittstelle repliziert wird. Die Schnittstelle Glogic_thresholdb hat den entgegengesetzten Ausgang aus der Tabelle in Glogic_ thresholda, damit das eine oder andere Schalterpaar arbeiten kann, anstatt gleichzeitig eingeschaltet zu werden.
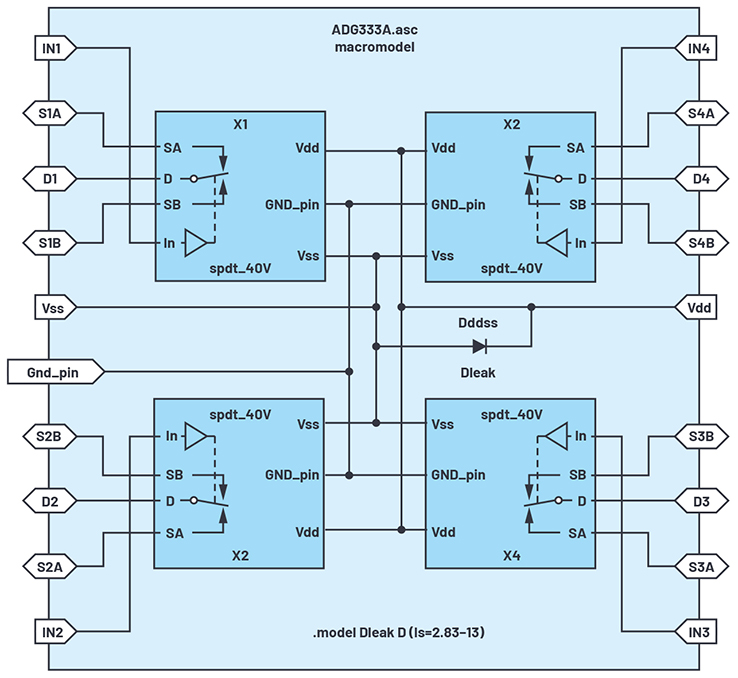 Abbildung 23. Schaltbild des Makromodells für den ADG333A
Ein alternatives ESD-Schutzkonzept umfasst Dioden von einem geschützten Pin zu sowohl VDD als auch zu VSS sowie eine Klemme zwischen VDD und VSS. Das Datenblatt liefert im Allgemeinen einen Einblick bezüglich des Schutzkonzepts, und Leckströme werden beiden Versorgungen zugeordnet.
Die Teilschaltung „spdt“ wird mit einem Symbol versehen und im Masterschaltbild ADG333A.asc von Abbildung 23 viermal verwendet.
Abbildung 24 ist das Schaltbild des Prüfaufbaus zur Verifizierung der endgültigen Makromodell-Ergebnisse.
Abbildung 23. Schaltbild des Makromodells für den ADG333A
Ein alternatives ESD-Schutzkonzept umfasst Dioden von einem geschützten Pin zu sowohl VDD als auch zu VSS sowie eine Klemme zwischen VDD und VSS. Das Datenblatt liefert im Allgemeinen einen Einblick bezüglich des Schutzkonzepts, und Leckströme werden beiden Versorgungen zugeordnet.
Die Teilschaltung „spdt“ wird mit einem Symbol versehen und im Masterschaltbild ADG333A.asc von Abbildung 23 viermal verwendet.
Abbildung 24 ist das Schaltbild des Prüfaufbaus zur Verifizierung der endgültigen Makromodell-Ergebnisse.
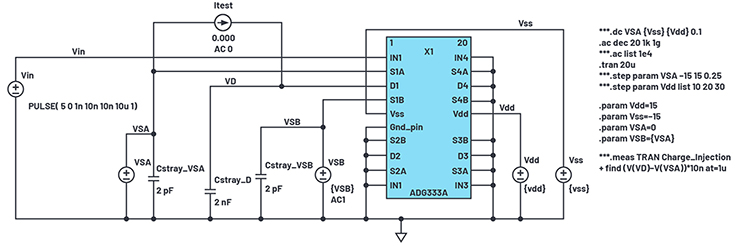 Abbildung 24. Prüfaufbau für das ADG333A-Makromodell
Zusammenfassung
Wir haben gesehen, wie sich ein ordentliches Makromodell für einen bestimmten Analogschalter realisieren lässt und wie man Parameter erhält, die ein paar verschiedene Halbleiterprozesse unterstützen, die zur Realisierung des physikalischen Bauteils verwendet werden. Das resultierende Makromodell zeigt Mängel auf, wie beispielsweise bezüglich des On-Widerstands und dessen Schwankungen, der Ladungsinjektion als Funktion des Versorgungs- und Signalspannungspegels, der parasitären Kapazitäten und deren Schwankungen über der Spannung, Verzögerungen der Logikschnittstelle und Leckströme. Wir hoffen, dass die Makromodelle bei der Simulation de tatsächlichen Verhaltensmerkmale von Analogschaltern hilfreich sind.
Nachtrag
Um LTspice herunterzuladen, besuchen Sie bitte analog.com/ltspice.
Hier ist die LTspice-Textdatei des Makromodell-Symbols, die unter dem Namen ADG333.asy gespeichert wird. Sie enthält Einzelheiten zur Simulation der Teilschaltung. Anstatt den Schema für ADG333.asc in jeden Schaltplan zu kopieren, der dieses Bauteil verwendet, verwenden wir ein Symbol, das darauf als .asy verweist. Innerhalb des ADG333-Symbols befinden sich einzelne Schaltersymbole. Dies ist das Symbol des Simulationsinhalts, das als spdt_40V.asc gespeichert wird. Das eigentliche Symbol wird als spdt_40V.asy gespeichert.
Abbildung 24. Prüfaufbau für das ADG333A-Makromodell
Zusammenfassung
Wir haben gesehen, wie sich ein ordentliches Makromodell für einen bestimmten Analogschalter realisieren lässt und wie man Parameter erhält, die ein paar verschiedene Halbleiterprozesse unterstützen, die zur Realisierung des physikalischen Bauteils verwendet werden. Das resultierende Makromodell zeigt Mängel auf, wie beispielsweise bezüglich des On-Widerstands und dessen Schwankungen, der Ladungsinjektion als Funktion des Versorgungs- und Signalspannungspegels, der parasitären Kapazitäten und deren Schwankungen über der Spannung, Verzögerungen der Logikschnittstelle und Leckströme. Wir hoffen, dass die Makromodelle bei der Simulation de tatsächlichen Verhaltensmerkmale von Analogschaltern hilfreich sind.
Nachtrag
Um LTspice herunterzuladen, besuchen Sie bitte analog.com/ltspice.
Hier ist die LTspice-Textdatei des Makromodell-Symbols, die unter dem Namen ADG333.asy gespeichert wird. Sie enthält Einzelheiten zur Simulation der Teilschaltung. Anstatt den Schema für ADG333.asc in jeden Schaltplan zu kopieren, der dieses Bauteil verwendet, verwenden wir ein Symbol, das darauf als .asy verweist. Innerhalb des ADG333-Symbols befinden sich einzelne Schaltersymbole. Dies ist das Symbol des Simulationsinhalts, das als spdt_40V.asc gespeichert wird. Das eigentliche Symbol wird als spdt_40V.asy gespeichert.
Über den Autor: Barry Harvey hat als Entwickler für Analog ICs gearbeitet und Hochgeschwindigkeits-Operationsverstärker, Spannungsreferenzen, Mixed-Signal-Schaltungen, Videoschaltungen, DSL-Leitungstreiber, DACs, Sample-and-Hold-Verstärker, Multipliziere und vieles mehr entworfen. Er hat einen Masterabschluss in Elektrotechnik (MSEE) von der Universität Stanford. Er ist Inhaber von mehr als 20 Patenten und hat ungefähr ebenso viele Artikel und Arbeiten veröffentlicht. Er ist zu erreichen unter barry.harvey@analog.com. / Copyright: © Analog Devices Inc.
- W/L, die Breite (W) geteilt durch die Länge (L) eines MOS-Bausteins. W/L ist die Größe oder relative Dicke des Bauteils.
- VTO, die Schwellenspannung; und Gamma, das den Wert für VTO entsprechend der Sperr- Vorspannung des Bauteils modifiziert. Die Sperr- Vorspannung ist die Spannung zwischen dem Einschaltelement und dessen Substratspannung; das Substrat ist im Schalter für den PMOS häufig mit der positiven Versorgungsspannung und für den NMOS mit der negativen Versorgungsspannung verbunden.
- KP, im Modell, auch als K’ oder K-prime bekannt. Dieser Parameter modelliert die Stärke des Prozesses und wird mit W/L multipliziert, um MOS-Ströme zu skalieren. Für einen gegebenen Prozess hat der NMOS ungefähr den 2,5-fachen KP-Wert des PMOS.
- RD, der parasitäre Widerstand des Drain-Anschlusses des Bauteils.
| Spannungs-knoten (V) | Bauteil-konstruktion | Gateoxid-Dicke (m) | VTO, n/p, V | Gamma, n/p, V0.5 | KP, n/p, µA/V2 | L, µ | RD, n/p, Ω |
| 40 | Drain-Drift-Region | 10-7 | 0,7/-0,9 | 0,4/-0,57 | 11/5 | 2 | ~80 % von RDS,ON |
| 15 | Soft-Drain-Diffusion | 4×10-8 | 0,7/-0,9 | 0,4/-0,57 | 22/10 | 1,5 | ~20 % von RDS,ON |
| 5 | Einfach | 1.4×10–8 | 0,7/-0,9 | 0,4/-0,57 | 80/28 | 0,5 | ~0 |
 Abbildung 1. RON in Abhängigkeit von VD (VS), duale Spannungsversorgung.
Es ist als allgemeiner Trend für diesen und alle anderen Analogschalter zu erkennen, dass höhere Versorgungsspannungen den On-Widerstand verringern. Je höher die an die MOS-Gates des Schalters angelegte Spannung ist, desto geringer wird der On-Widerstand. Zu beobachten auch eine deutliche Veränderung des Widerstands über den analogen Pegel. In den N-Regionen ist der NMOS-Transistor eines Schalters vollständig eingeschaltet. Wenn die Analogspannung über die negative Linie ansteigt, schaltet sich der PMOS-Transistor ein und trägt zur Verringerung des Gesamt-On-Widerstands bei. Der Wendepunkt in der N-Region liegt ungefähr eine PMOS VTO über der negativen Versorgungsspannung.
In gleicher Weise ist in den P-Regionen der PMOS-Baustein des Schalters vollständig eingeschaltet, und der NMOS beginnt, den PMOS-Transistor ungefähr ab einer NMOS-VTO unterhalb der positiven Versorgungsspannung zu unterstützen.
Die M-Regionen befinden sich in der Mitte der N- und P-Regionen, in welcher der NMOS und der PMOS parallel arbeiten, aber je nach dem analogen Signalpegel zwischen den Versorgungen einen unterschiedlichen On-Widerstand aufweisen.
Um mit der Kurvenanpassung zu beginnen, schätzen wir zunächst die Größe eines jeden einzelnen Transistors. Die Kleinspannungskurve liefert die beste Kurvenanpassung für RDS,ON des Transistors. In Region N, mit dem Analogsignal an der negativen Versorgungsspannung, ist das PMOS-Bauelement ausgeschaltet und RON des Bauteils ist gleich dem RON des NMOS-Transistors. Mit
Abbildung 1. RON in Abhängigkeit von VD (VS), duale Spannungsversorgung.
Es ist als allgemeiner Trend für diesen und alle anderen Analogschalter zu erkennen, dass höhere Versorgungsspannungen den On-Widerstand verringern. Je höher die an die MOS-Gates des Schalters angelegte Spannung ist, desto geringer wird der On-Widerstand. Zu beobachten auch eine deutliche Veränderung des Widerstands über den analogen Pegel. In den N-Regionen ist der NMOS-Transistor eines Schalters vollständig eingeschaltet. Wenn die Analogspannung über die negative Linie ansteigt, schaltet sich der PMOS-Transistor ein und trägt zur Verringerung des Gesamt-On-Widerstands bei. Der Wendepunkt in der N-Region liegt ungefähr eine PMOS VTO über der negativen Versorgungsspannung.
In gleicher Weise ist in den P-Regionen der PMOS-Baustein des Schalters vollständig eingeschaltet, und der NMOS beginnt, den PMOS-Transistor ungefähr ab einer NMOS-VTO unterhalb der positiven Versorgungsspannung zu unterstützen.
Die M-Regionen befinden sich in der Mitte der N- und P-Regionen, in welcher der NMOS und der PMOS parallel arbeiten, aber je nach dem analogen Signalpegel zwischen den Versorgungen einen unterschiedlichen On-Widerstand aufweisen.
Um mit der Kurvenanpassung zu beginnen, schätzen wir zunächst die Größe eines jeden einzelnen Transistors. Die Kleinspannungskurve liefert die beste Kurvenanpassung für RDS,ON des Transistors. In Region N, mit dem Analogsignal an der negativen Versorgungsspannung, ist das PMOS-Bauelement ausgeschaltet und RON des Bauteils ist gleich dem RON des NMOS-Transistors. Mit
 setzen wir unter Verwendung der typischen 40-V-NMOS-Prozesswerte aus der Kurve in Abbildung 1 einen RDS,ON = 38 Ω, und unter Verwendung der angegebenen Prozessgrößen finden wir WNMOS = 2 µA/(38 Ω × (11 × 10-6 µA/V2) × (10 V - 0,7 V)) = 514 µm. Der PMOS-Schalter hätte somit einen On-Widerstand von 47 Ω aus der obigen Kurve und damit eine Breite von 936 µm.
setzen wir unter Verwendung der typischen 40-V-NMOS-Prozesswerte aus der Kurve in Abbildung 1 einen RDS,ON = 38 Ω, und unter Verwendung der angegebenen Prozessgrößen finden wir WNMOS = 2 µA/(38 Ω × (11 × 10-6 µA/V2) × (10 V - 0,7 V)) = 514 µm. Der PMOS-Schalter hätte somit einen On-Widerstand von 47 Ω aus der obigen Kurve und damit eine Breite von 936 µm.
 Abbildung 2. Testschaltung für den On-Widerstand
Ich habe die in Abbildung 2 gezeigte LTspice -Testschaltung verwendet. Zu beachten ist, dass die Parameter RDN und RDP, die parasitären Drain-Widerstände, einen eher moderaten Wert haben. Ich habe mit einem Wert von 1 µ begonnen, was zu einer Verlangsamung der Simulatorkonvergenz führte. Ein RDN-Wert von 1 ermöglicht eine angemessene Simulationsgeschwindigkeit. Das Hinzufügen von RCONVERGENCE hat das Simulationsrauschen und die Simulationsgeschwindigkeit verbessert, indem dem Umschaltknoten eine konvergenzfähige Leitfähigkeit verliehen wurde. Für die Messung des On-Widerstands habe ich eine potentialfreie Stromquelle getestet.
Abbildung 2. Testschaltung für den On-Widerstand
Ich habe die in Abbildung 2 gezeigte LTspice -Testschaltung verwendet. Zu beachten ist, dass die Parameter RDN und RDP, die parasitären Drain-Widerstände, einen eher moderaten Wert haben. Ich habe mit einem Wert von 1 µ begonnen, was zu einer Verlangsamung der Simulatorkonvergenz führte. Ein RDN-Wert von 1 ermöglicht eine angemessene Simulationsgeschwindigkeit. Das Hinzufügen von RCONVERGENCE hat das Simulationsrauschen und die Simulationsgeschwindigkeit verbessert, indem dem Umschaltknoten eine konvergenzfähige Leitfähigkeit verliehen wurde. Für die Messung des On-Widerstands habe ich eine potentialfreie Stromquelle getestet.
 Abbildung 3. Simulationsergebnisse für den On-Widerstand mit anfänglichen Modellwerten.
Abbildung 3 zeigt die Simulationsergebnisse für verschiedene Versorgungsspannungen.
Dies ist schon mal ein guter Anfang. Der Knick am unteren Ende des Spannungsbereichs für VS = 30 V liegt bei 3,6 V in der Simulation und bei 2,7 V im Datenblatt. Dies legt nahe, den PMOS-VTO-Wert zu reduzieren, allerdings ist 0,9 V bereits ein realistisches Minimum. Besser ist es daher, den Gamma-Wert des PMOS anzupassen, der ohnehin nur ein Schätzwert war.
Der Knick in der Nähe der maximalen Versorgungsspannung liegt 2,5 V unterhalb der 30-V-Versorgungsspannung, während er im Datenblatt ~1 V betragen sollte. Verschiedene Gamma-Werte führten zu einer Überhöhung der Knickspannung von der Versorgungsspannung; wir setzen daher einfach die NMOS-VTO auf 1 V und dessen Gamma auf null. Ein Gamma von Null ist nicht zu erwarten, aber wir versuchen nur, uns der Kurve anzupassen.
Abbildung 3. Simulationsergebnisse für den On-Widerstand mit anfänglichen Modellwerten.
Abbildung 3 zeigt die Simulationsergebnisse für verschiedene Versorgungsspannungen.
Dies ist schon mal ein guter Anfang. Der Knick am unteren Ende des Spannungsbereichs für VS = 30 V liegt bei 3,6 V in der Simulation und bei 2,7 V im Datenblatt. Dies legt nahe, den PMOS-VTO-Wert zu reduzieren, allerdings ist 0,9 V bereits ein realistisches Minimum. Besser ist es daher, den Gamma-Wert des PMOS anzupassen, der ohnehin nur ein Schätzwert war.
Der Knick in der Nähe der maximalen Versorgungsspannung liegt 2,5 V unterhalb der 30-V-Versorgungsspannung, während er im Datenblatt ~1 V betragen sollte. Verschiedene Gamma-Werte führten zu einer Überhöhung der Knickspannung von der Versorgungsspannung; wir setzen daher einfach die NMOS-VTO auf 1 V und dessen Gamma auf null. Ein Gamma von Null ist nicht zu erwarten, aber wir versuchen nur, uns der Kurve anzupassen.
 Abbildung 4. Simulationsergebnisse für den On-Widerstand bei Variation von gamma-p
Abbildung 4 zeigt die Simulationsergebnisse aus diesen Werten, wobei der Gamma-Wert des PMOS für verschiedene Versorgungsspannungen stufenweise erhöht wurde. Wir konzentrieren uns auf die 30-V-Kurven, bei denen der Gamma-Effekt maximal ist im Vergleich zu niedrigeren Versorgungsspannungen
Aus den abgestuften Kurven wählen wir ein PMOS-Gamma = 0,4.
Weiter zu RON. Es ist zu beachten, dass die 10 V-Kurven repräsentativ für die Datenblattkurve an den Extrema der Versorgungsspannung sind, die Simulation jedoch einen zu niedrigen RON für die 20-V- und 30-V-Kurven ergibt. Die RONs entsprechen RDS,ON(NMOS) + RD(NMOS) im Bereich nahe der positiven Versorgungsspannung und RDS,ON(PMOS) + RD(PMOS) Im Bereich nahe der positiven Versorgungsspannung. Bei hohen Versorgungsspannungen ist der Parameter RD signifikanter als W/L, während bei niedrigen Versorgungsspannungen W/L dominiert.
Abbildung 4. Simulationsergebnisse für den On-Widerstand bei Variation von gamma-p
Abbildung 4 zeigt die Simulationsergebnisse aus diesen Werten, wobei der Gamma-Wert des PMOS für verschiedene Versorgungsspannungen stufenweise erhöht wurde. Wir konzentrieren uns auf die 30-V-Kurven, bei denen der Gamma-Effekt maximal ist im Vergleich zu niedrigeren Versorgungsspannungen
Aus den abgestuften Kurven wählen wir ein PMOS-Gamma = 0,4.
Weiter zu RON. Es ist zu beachten, dass die 10 V-Kurven repräsentativ für die Datenblattkurve an den Extrema der Versorgungsspannung sind, die Simulation jedoch einen zu niedrigen RON für die 20-V- und 30-V-Kurven ergibt. Die RONs entsprechen RDS,ON(NMOS) + RD(NMOS) im Bereich nahe der positiven Versorgungsspannung und RDS,ON(PMOS) + RD(PMOS) Im Bereich nahe der positiven Versorgungsspannung. Bei hohen Versorgungsspannungen ist der Parameter RD signifikanter als W/L, während bei niedrigen Versorgungsspannungen W/L dominiert.
 Abbildung 5. Simulationsergebnisse für den On-Widerstand mit festgelegtem WN.
Wir müssen hier mit zwei Variablen jonglieren, was zu mühsam ist. Es ist festzustellen, dass sich der RON-Wert mit der Versorgungsspannung ändert, weil der NMOS variabel angereichert wird, der RD-Wert sich jedoch nicht mit der Versorgungsspannung ändert (okay, bei Drains mit Drift-Regionen tut er dies wahrscheinlich doch, aber wir wollen es hier einfach halten).
Wenn wir den Unterschied für RON im Datenblatt zwischen den Versorgungsspannungen 10 V und 30 V beachten (11,4 Ω), können wir dies mit den obigen Kurven vergleichen, wobei wir ausschließlich WN (Breite des NMOS im Schalter) abstufen. Nach ein paar Iterationen von WN in den Simulationen ist klar, dass wir WN = 1170 µm benötigen, um das erforderlichen ΔRON zu erhalten, also weitaus mehr als die anfängliche Schätzung. Abbildung 5 zeigt unsere aktuellen Ergebnisse.
Während der RON des NMOS die richtige Empfindlichkeit gegenüber der Versorgungsspannung aufweist, haben die Kurven bei null Volt einen zu niedrigen Wert, und wir müssen den festgelegten Wert für RDN erhöhen. Nach Erhöhung und Iteration von RDN erhalten wir einen besten Wert von RDN = 22 Ω, und die resultierenden Kurven sind in Abbildung 6 dargestellt.
Abbildung 5. Simulationsergebnisse für den On-Widerstand mit festgelegtem WN.
Wir müssen hier mit zwei Variablen jonglieren, was zu mühsam ist. Es ist festzustellen, dass sich der RON-Wert mit der Versorgungsspannung ändert, weil der NMOS variabel angereichert wird, der RD-Wert sich jedoch nicht mit der Versorgungsspannung ändert (okay, bei Drains mit Drift-Regionen tut er dies wahrscheinlich doch, aber wir wollen es hier einfach halten).
Wenn wir den Unterschied für RON im Datenblatt zwischen den Versorgungsspannungen 10 V und 30 V beachten (11,4 Ω), können wir dies mit den obigen Kurven vergleichen, wobei wir ausschließlich WN (Breite des NMOS im Schalter) abstufen. Nach ein paar Iterationen von WN in den Simulationen ist klar, dass wir WN = 1170 µm benötigen, um das erforderlichen ΔRON zu erhalten, also weitaus mehr als die anfängliche Schätzung. Abbildung 5 zeigt unsere aktuellen Ergebnisse.
Während der RON des NMOS die richtige Empfindlichkeit gegenüber der Versorgungsspannung aufweist, haben die Kurven bei null Volt einen zu niedrigen Wert, und wir müssen den festgelegten Wert für RDN erhöhen. Nach Erhöhung und Iteration von RDN erhalten wir einen besten Wert von RDN = 22 Ω, und die resultierenden Kurven sind in Abbildung 6 dargestellt.
 Abbildung 6. Simulationsergebnisse für den On-Widerstand mit festgelegtem RDN. / Abbildung 7. Simulationsergebnisse für den On-Widerstand mit festgelegtem WP und RDP.
Als Nächstes bestimmen wir WP (die Breite des PMOS im Schalter), um RON bei maximaler Spannung zu simulieren, und erhalten WP = 1700 µm, wiederum eine ganze Menge mehr als anfänglich vermutet. Mit einem ebenfalls auf 22 Ω festgelegten RDP erhalten wir die endgültige RON-Kurve in Abbildung 7.
Hier sehen wir eine ziemlich gute Übereinstimmung; es gibt nur einige wenige Merkmale, die sich vom Datenblatt unterscheiden. Zum einen sind die Wendepunkte in der Datenblattkurve glatt, während sie in der Simulation wirklich spitz sind. Dies liegt wahrscheinlich daran, dass das verwendete einfache MOS-Modell keine Unterschwelleneffekte unterstützt und das simulierte Bauelement sich bei VTO wirklich abschaltet. Reale Bauelemente sind bei VTO nicht ausgeschaltet, sondern verringern den Strom allmählich unterhalb dieser Spannung.
Ein weiterer Fehler ist in der 30-V-Kurve am deutlichsten zu erkennen. Der RON ist in der Mitte der Versorgungsspannung gegenüber dem Datenblatt um 15 % niedriger. Möglicherweise ist dies auf die ebenfalls nicht modellierten JFET-Effekte innerhalb der Drain-Drift-Region zurückzuführen.
Was die Temperatur betrifft, so gibt es eine gewisse, aber nicht allzu starke Übereinstimmung, wie in Abbildung 8 zu sehen ist.
Abbildung 6. Simulationsergebnisse für den On-Widerstand mit festgelegtem RDN. / Abbildung 7. Simulationsergebnisse für den On-Widerstand mit festgelegtem WP und RDP.
Als Nächstes bestimmen wir WP (die Breite des PMOS im Schalter), um RON bei maximaler Spannung zu simulieren, und erhalten WP = 1700 µm, wiederum eine ganze Menge mehr als anfänglich vermutet. Mit einem ebenfalls auf 22 Ω festgelegten RDP erhalten wir die endgültige RON-Kurve in Abbildung 7.
Hier sehen wir eine ziemlich gute Übereinstimmung; es gibt nur einige wenige Merkmale, die sich vom Datenblatt unterscheiden. Zum einen sind die Wendepunkte in der Datenblattkurve glatt, während sie in der Simulation wirklich spitz sind. Dies liegt wahrscheinlich daran, dass das verwendete einfache MOS-Modell keine Unterschwelleneffekte unterstützt und das simulierte Bauelement sich bei VTO wirklich abschaltet. Reale Bauelemente sind bei VTO nicht ausgeschaltet, sondern verringern den Strom allmählich unterhalb dieser Spannung.
Ein weiterer Fehler ist in der 30-V-Kurve am deutlichsten zu erkennen. Der RON ist in der Mitte der Versorgungsspannung gegenüber dem Datenblatt um 15 % niedriger. Möglicherweise ist dies auf die ebenfalls nicht modellierten JFET-Effekte innerhalb der Drain-Drift-Region zurückzuführen.
Was die Temperatur betrifft, so gibt es eine gewisse, aber nicht allzu starke Übereinstimmung, wie in Abbildung 8 zu sehen ist.
 Abbildung 8. Ergebnisse aus Simulation und Datenblatt für RON über die Temperatur.
Die Simulation zeigt eine Temperaturabhängigkeit, die allerdings nicht so stark ist wie die in den Datenblattkurven. Im Simulationsmodell haben die RD-Terme keine Temperaturkoeffizienten. Die RDs könnten durch externe Widerstände mit korrekten Temperaturkoeffizienten modelliert werden, der Einfachheit halber belassen wir es aber dabei.
Gewinnung der LTspice-Modellparameter für die Ladungsinjektion
Wenn MOS-Transistoren abschalten, muss die Ladung im Kanal irgendwo hingehen, so dass sie aus den Drain- und Source-Anschlüssen austritt. Wenn ein Analogschalter ausgeschaltet wird, tritt auch Ladung aus, was als Ladungsinjektion bezeichnet wird. Eine gebräuchliche Art, diese zu messen, besteht darin, an einem Ende eines Einschalters eine feste Spannung und am anderen Ende einen großen Kondensator anzulegen.
Abbildung 8. Ergebnisse aus Simulation und Datenblatt für RON über die Temperatur.
Die Simulation zeigt eine Temperaturabhängigkeit, die allerdings nicht so stark ist wie die in den Datenblattkurven. Im Simulationsmodell haben die RD-Terme keine Temperaturkoeffizienten. Die RDs könnten durch externe Widerstände mit korrekten Temperaturkoeffizienten modelliert werden, der Einfachheit halber belassen wir es aber dabei.
Gewinnung der LTspice-Modellparameter für die Ladungsinjektion
Wenn MOS-Transistoren abschalten, muss die Ladung im Kanal irgendwo hingehen, so dass sie aus den Drain- und Source-Anschlüssen austritt. Wenn ein Analogschalter ausgeschaltet wird, tritt auch Ladung aus, was als Ladungsinjektion bezeichnet wird. Eine gebräuchliche Art, diese zu messen, besteht darin, an einem Ende eines Einschalters eine feste Spannung und am anderen Ende einen großen Kondensator anzulegen.
 Abbildung 9. Simulationsaufbau für die Ladungsinjektion.
Beim Ausschalten wird die Ladung vom Kondensator aufgefangen und ein kleiner Spannungssprung entsteht. Wir fügen nun die Gate-Oxiddicke TOX = 1 × 10-7 zu den MOS-Modellen hinzu (die Gate-Kapazität ist die größte Quelle der Ladungsinjektion). Unser Simulationsaufbau ist in Abbildung 9 dargestellt.
Abbildung 9. Simulationsaufbau für die Ladungsinjektion.
Beim Ausschalten wird die Ladung vom Kondensator aufgefangen und ein kleiner Spannungssprung entsteht. Wir fügen nun die Gate-Oxiddicke TOX = 1 × 10-7 zu den MOS-Modellen hinzu (die Gate-Kapazität ist die größte Quelle der Ladungsinjektion). Unser Simulationsaufbau ist in Abbildung 9 dargestellt.
 Abbildung 10. Wellenformen bei der Simulation der Ladungsinjektion.
Bei der Testschaltung für die Ladungsinjektion im Datenblatt wird eine Spannungsquelle am Anschluss D und ein Kondensator Cl am Anschluss S des Schalters platziert. Wenn die Schalttransistoren abgeschaltet werden, wird Cl isoliert und nimmt die von den Schaltern zugeführte Ladung auf. Die Wellenform eines solchen Ereignisses mit auf 24 V gehaltener Spannung VD bei einer 30-V-Versorgung ist in Abbildung 10 dargestellt.
Die injizierte Ladung entspricht dem Spannungssprung zwischen V(S) und V(D) multipliziert mit dem 10 nF-Haltekondensator. Wir können die Schaltspannung VD über die Versorgungsspannung stufenweise erhöhen und die meas-Anweisung verwenden, um den Wert der Ladungsinjektion bei jeder Spannung zu erfassen. Abbildung 11 zeigt die Datenblattkurve und die simulierten Ergebnisse.
Abbildung 10. Wellenformen bei der Simulation der Ladungsinjektion.
Bei der Testschaltung für die Ladungsinjektion im Datenblatt wird eine Spannungsquelle am Anschluss D und ein Kondensator Cl am Anschluss S des Schalters platziert. Wenn die Schalttransistoren abgeschaltet werden, wird Cl isoliert und nimmt die von den Schaltern zugeführte Ladung auf. Die Wellenform eines solchen Ereignisses mit auf 24 V gehaltener Spannung VD bei einer 30-V-Versorgung ist in Abbildung 10 dargestellt.
Die injizierte Ladung entspricht dem Spannungssprung zwischen V(S) und V(D) multipliziert mit dem 10 nF-Haltekondensator. Wir können die Schaltspannung VD über die Versorgungsspannung stufenweise erhöhen und die meas-Anweisung verwenden, um den Wert der Ladungsinjektion bei jeder Spannung zu erfassen. Abbildung 11 zeigt die Datenblattkurve und die simulierten Ergebnisse.
 Abbildung 11. Wellenformen für die Ladungsinjektion aus Datenblatt und Simulation
Unser einfaches MOS-Modell bildet die Form der Datenblattkurve nicht sehr gut nach, aber die Spitze-Spitze-Ladungsinjektion beträgt 32 pC in den Datenblattkurven und 31 pC in der Simulation. Dies ist schon überraschend nahe dran, aber wenn es sein müsste, könnten wir noch TOX optimieren, um die Simulationsergebnisse zu perfektionieren.
Es besteht ein Versatz zwischen den Kurven, den wir mit CCHARGE_INJECTION ausgleichen können. Nach Herumspielen mit einigen Werten wählen wir als optimalen Wert CCHARGE_INJECTION = 0,28 pF. Wenn eine Verschiebung mit entgegengesetzter Polarität erforderlich wäre, würde CCHARGE_INJECTION wieder mit dem Knoten PMOS_on_when_low verbunden werden.
Der Anpassungskondensator CCHARGE_INJECTION war eine bequeme Möglichkeit, die Ladungsinjektion gegenüber der Simulationskurve der analogen Spannung auszugleichen. Was wäre, wenn die simulierte Spitze-Spitze-Injektion zu klein wäre? Nun, der größte Teil der Ladungsinjektion besteht zumeist aus den Schwankungen der Gatespannung der Schalter, welche Ladung durch die Gatekanal-Kapazität der Schalttransistoren schicken. Wenn wir eine zu geringe Injektion simulieren, können wir einfach einen oder beide Gate-Bereiche vergrößern. Dazu müssten wir die Parameter L und W eines Schaltgerätes um den gleichen Faktor erhöhen, wobei darauf zu achten ist, dass das Verhältnis W/L-Verhältnis, das den On-Widerstand festlegt, nicht verändert wird. Anstatt CCHARGE_INJECTION zu verwenden, hätten wir die auch die Werte W und L des NMOS erhöhen können.
Alternativ könnten wir den Wert für TOX in jedem Bauteil anpassen, um eine bessere Korrelation der Ladungsinjektion zu erhalten. Das wäre physikalisch nicht möglich – aber es ist ja auch nur eine Simulation. Bei den einfachen Modellen, die wir verwenden, beeinflusst TOX andere Schaltungsverhalten nicht.
Bestimmung von LTspice-Modell-Parametern für Kapazitäten
Nachdem wir die Parameter für gute Simulationsergebnisse für RON und Ladungsinjektion eingestellt haben, simulieren wir nun die Kapazitäten der Anschlüsse S und D.
Ein wichtiger Punkt ist, dass sowohl der Drain- als auch der Source-Bereich von Hochspannungs-MOS-Schaltern Driftbereiche aufweisen müssen. Als Schalter kann man den funktionellen Unterschied zwischen Source- und Drain-Anschlüssen nicht erkennen, und das Substrat- Potenzial gegenüber den Drain und Source-Anschlüssen erfordert die entsprechenden Driftregionen in beiden. Dies gilt auch für die Soft-Diffusionen im mittleren Spannungsbereich, die jedoch bei Kleinspannungs-MOS nicht vorhanden sind. Wir haben den verteilten Widerstand in der Driftregion, der sowohl im Drain als auch in der Source vorhanden wäre, in RD zusammengefasst, was bei Schaltern gut funktioniert, jedoch nicht bei Transistoren in der Sättigung.
Abbildung 12 zeigt unseren Simulationsaufbau.
Abbildung 11. Wellenformen für die Ladungsinjektion aus Datenblatt und Simulation
Unser einfaches MOS-Modell bildet die Form der Datenblattkurve nicht sehr gut nach, aber die Spitze-Spitze-Ladungsinjektion beträgt 32 pC in den Datenblattkurven und 31 pC in der Simulation. Dies ist schon überraschend nahe dran, aber wenn es sein müsste, könnten wir noch TOX optimieren, um die Simulationsergebnisse zu perfektionieren.
Es besteht ein Versatz zwischen den Kurven, den wir mit CCHARGE_INJECTION ausgleichen können. Nach Herumspielen mit einigen Werten wählen wir als optimalen Wert CCHARGE_INJECTION = 0,28 pF. Wenn eine Verschiebung mit entgegengesetzter Polarität erforderlich wäre, würde CCHARGE_INJECTION wieder mit dem Knoten PMOS_on_when_low verbunden werden.
Der Anpassungskondensator CCHARGE_INJECTION war eine bequeme Möglichkeit, die Ladungsinjektion gegenüber der Simulationskurve der analogen Spannung auszugleichen. Was wäre, wenn die simulierte Spitze-Spitze-Injektion zu klein wäre? Nun, der größte Teil der Ladungsinjektion besteht zumeist aus den Schwankungen der Gatespannung der Schalter, welche Ladung durch die Gatekanal-Kapazität der Schalttransistoren schicken. Wenn wir eine zu geringe Injektion simulieren, können wir einfach einen oder beide Gate-Bereiche vergrößern. Dazu müssten wir die Parameter L und W eines Schaltgerätes um den gleichen Faktor erhöhen, wobei darauf zu achten ist, dass das Verhältnis W/L-Verhältnis, das den On-Widerstand festlegt, nicht verändert wird. Anstatt CCHARGE_INJECTION zu verwenden, hätten wir die auch die Werte W und L des NMOS erhöhen können.
Alternativ könnten wir den Wert für TOX in jedem Bauteil anpassen, um eine bessere Korrelation der Ladungsinjektion zu erhalten. Das wäre physikalisch nicht möglich – aber es ist ja auch nur eine Simulation. Bei den einfachen Modellen, die wir verwenden, beeinflusst TOX andere Schaltungsverhalten nicht.
Bestimmung von LTspice-Modell-Parametern für Kapazitäten
Nachdem wir die Parameter für gute Simulationsergebnisse für RON und Ladungsinjektion eingestellt haben, simulieren wir nun die Kapazitäten der Anschlüsse S und D.
Ein wichtiger Punkt ist, dass sowohl der Drain- als auch der Source-Bereich von Hochspannungs-MOS-Schaltern Driftbereiche aufweisen müssen. Als Schalter kann man den funktionellen Unterschied zwischen Source- und Drain-Anschlüssen nicht erkennen, und das Substrat- Potenzial gegenüber den Drain und Source-Anschlüssen erfordert die entsprechenden Driftregionen in beiden. Dies gilt auch für die Soft-Diffusionen im mittleren Spannungsbereich, die jedoch bei Kleinspannungs-MOS nicht vorhanden sind. Wir haben den verteilten Widerstand in der Driftregion, der sowohl im Drain als auch in der Source vorhanden wäre, in RD zusammengefasst, was bei Schaltern gut funktioniert, jedoch nicht bei Transistoren in der Sättigung.
Abbildung 12 zeigt unseren Simulationsaufbau.
 Abbildung 12. Simulationsaufbau für die Ermittlung der Off-Kapazität
In LTspice kann man eine .ac-Analyse nur auf einer Frequenz ausführen, indem man die Listenoption in .ac verwendet, dabei aber nur ein Frequenzargument angibtn (hier 1 MHz). Anschließend lässt man eine .step VSOURCE-Gleichspannung über den Versorgungsspannungsbereich laufen, um einen Verlauf der Kapazität gegenüber der Spannung zu erhalten.
Der D-Anschluss des Ausschalters wird auf mittlerer Versorgungsspannung gehalten. Der S-Anschluss, der hier zur Vermeidung von Verwechslungen mit VS in Source umbenannt wurde, wird von einer Gleichspannungsquelle, die 0 V bis VS überstreicht, mit einer Wechselspannungsansteuerung von 1 V angesteuert. Die Kapazität wird von I(VSOURCE)/(2 × π × 1 MHz × 1 V) abgeleitet. Die Logikansteuerung V1 wird auf 0 V geändert, um die Transistoren auszuschalten.
Die Drain- und Source-Kapazitäten zum Substrat (Bulk) werden in der Modellerklärung als CBD bzw. CBS bezeichnet.
Das Modell verfügt über eingebaute Standardkonzentrationen, eine interne Spannung und einen Exponenten, die die Spannungen über CBD und CBS variabel machen. Da diese symmetrisch sind, würden die Drain- und Source-Kapazitäten gleich gesetzt werden. Da der PMOS eine andere Breite als der NMOS hat, ist darüber hinaus das Verhältnis von CBD,NMOS/CBD,PMOS = CBS,NMOS/CBS,PMOS = WN/WP, welches wir bei der Modellierung des On-Widerstands ermittelt haben. Abbildung 13 zeigt die Simulationsergebnisse.
Abbildung 12. Simulationsaufbau für die Ermittlung der Off-Kapazität
In LTspice kann man eine .ac-Analyse nur auf einer Frequenz ausführen, indem man die Listenoption in .ac verwendet, dabei aber nur ein Frequenzargument angibtn (hier 1 MHz). Anschließend lässt man eine .step VSOURCE-Gleichspannung über den Versorgungsspannungsbereich laufen, um einen Verlauf der Kapazität gegenüber der Spannung zu erhalten.
Der D-Anschluss des Ausschalters wird auf mittlerer Versorgungsspannung gehalten. Der S-Anschluss, der hier zur Vermeidung von Verwechslungen mit VS in Source umbenannt wurde, wird von einer Gleichspannungsquelle, die 0 V bis VS überstreicht, mit einer Wechselspannungsansteuerung von 1 V angesteuert. Die Kapazität wird von I(VSOURCE)/(2 × π × 1 MHz × 1 V) abgeleitet. Die Logikansteuerung V1 wird auf 0 V geändert, um die Transistoren auszuschalten.
Die Drain- und Source-Kapazitäten zum Substrat (Bulk) werden in der Modellerklärung als CBD bzw. CBS bezeichnet.
Das Modell verfügt über eingebaute Standardkonzentrationen, eine interne Spannung und einen Exponenten, die die Spannungen über CBD und CBS variabel machen. Da diese symmetrisch sind, würden die Drain- und Source-Kapazitäten gleich gesetzt werden. Da der PMOS eine andere Breite als der NMOS hat, ist darüber hinaus das Verhältnis von CBD,NMOS/CBD,PMOS = CBS,NMOS/CBS,PMOS = WN/WP, welches wir bei der Modellierung des On-Widerstands ermittelt haben. Abbildung 13 zeigt die Simulationsergebnisse.
 Abbildung 13. Ergebnisse für die Off-Kapazität in Abhängigkeit von der Gleichspannung bei VS = 12 V (links) und 30 V (rechts).
Angezeigt wird I(VSOURCE)/(2 × π × 1 MHz), was eine Kapazität darstellt. LTspice weiß dies allerdings nicht und zeigt pA statt pF an.
Leider haben wir keine Datenblattkurven zum Vergleich zur Verfügung. Aus der Spezifikationstabelle im Datenblatt wissen wir, dass die Kapazität - wahrscheinlich in der Mitte der Versorgungsspannungen, jedoch nicht im Datenblatt angegeben - typischerweise 7 pF bei Versorgung mit 30 V und 12 pF bei Versorgung mit 12 V beträgt. Ich habe die CBs angepasst, um die 7 pF-Kurve bei 30 V zu erhalten, aber nur 10 pF bei einer 12-V-Versorgung simuliert. Nach Herumspielen mit den internen Potenzial- und Kapazitätsformel-Exponenten lässt das verwendete Modell keine Flexibilität zur Verbesserung der 12 V/30 V-Übereinstimmung zu.
Abbildung 14 zeigt den Simulationsaufbau für die Off-State-Kapazität.
Abbildung 13. Ergebnisse für die Off-Kapazität in Abhängigkeit von der Gleichspannung bei VS = 12 V (links) und 30 V (rechts).
Angezeigt wird I(VSOURCE)/(2 × π × 1 MHz), was eine Kapazität darstellt. LTspice weiß dies allerdings nicht und zeigt pA statt pF an.
Leider haben wir keine Datenblattkurven zum Vergleich zur Verfügung. Aus der Spezifikationstabelle im Datenblatt wissen wir, dass die Kapazität - wahrscheinlich in der Mitte der Versorgungsspannungen, jedoch nicht im Datenblatt angegeben - typischerweise 7 pF bei Versorgung mit 30 V und 12 pF bei Versorgung mit 12 V beträgt. Ich habe die CBs angepasst, um die 7 pF-Kurve bei 30 V zu erhalten, aber nur 10 pF bei einer 12-V-Versorgung simuliert. Nach Herumspielen mit den internen Potenzial- und Kapazitätsformel-Exponenten lässt das verwendete Modell keine Flexibilität zur Verbesserung der 12 V/30 V-Übereinstimmung zu.
Abbildung 14 zeigt den Simulationsaufbau für die Off-State-Kapazität.
 Abbildung 14. Simulationsaufbau für die Off-State-Kapazität.
Hier ist der rechte Schalter eines vollen spdt-Schalters eingeschaltet, während der linke Schalter ausgeschaltet und an eine VS/2-Quelle angeschlossen ist. Die Kapazitäten der rechten Hälfte des linken Schalters und die vollen Kapazitäten des rechten Schalters sowie die unvermeidlichen parasitären Kapazitäten an den Anschlüssen D und S werden alle parallel geschaltet und von unserem 1-MHz-Testsignal an der Vs-Quelle angesteuert, deren Gleichspannungspegel von Masse bis VS gestuft ist. Abbildung 15 zeigt die Ergebnisse.
Abbildung 14. Simulationsaufbau für die Off-State-Kapazität.
Hier ist der rechte Schalter eines vollen spdt-Schalters eingeschaltet, während der linke Schalter ausgeschaltet und an eine VS/2-Quelle angeschlossen ist. Die Kapazitäten der rechten Hälfte des linken Schalters und die vollen Kapazitäten des rechten Schalters sowie die unvermeidlichen parasitären Kapazitäten an den Anschlüssen D und S werden alle parallel geschaltet und von unserem 1-MHz-Testsignal an der Vs-Quelle angesteuert, deren Gleichspannungspegel von Masse bis VS gestuft ist. Abbildung 15 zeigt die Ergebnisse.
 Abbildung 15. Simulationsergebnisse On-Kapazität vs. Gleichspannung bei VS = 12 V (links) und 30 V (rechts).
Die Simulation ergibt 29,5 pF bzw. 21,4 pF, während im Datenblatt 26 pF bzw. 25 pF angegeben sind. Angesichts der üblichen Kapazitätsschwankungen von Leiterplatten-Layouts können wir dies als nahe genug betrachten.
Leckströme
Die Datenblattkurven zeigen bei 25 °C spannungsabhängige Leckströme im pA-Bereich, während die Datenblattspezifikation lediglich Leckströme im Bereich von einigen hundert pA garantiert. Ich bin mehr von den Ergebnissen der Kurven bei 25 °C beeindruckt. Die geringen Leckströme wurden bei diesem Gerät offenbar nicht für wichtig genug gehalten, um sie beim Test zu garantieren. Fairerweise muss man sagen, dass die Messung einzelner pA einen hohen technischen Entwicklungsaufwand und lange Testzeiten erfordert.
Bei 85 °C werden einige nA garantiert (die effizient gemessen werden können) mit einem typischen Ergebnis im Bereich von einigen hundert pA. Ich werde diese typischen Ergebnisse als gut akzeptieren.
Abbildung 15. Simulationsergebnisse On-Kapazität vs. Gleichspannung bei VS = 12 V (links) und 30 V (rechts).
Die Simulation ergibt 29,5 pF bzw. 21,4 pF, während im Datenblatt 26 pF bzw. 25 pF angegeben sind. Angesichts der üblichen Kapazitätsschwankungen von Leiterplatten-Layouts können wir dies als nahe genug betrachten.
Leckströme
Die Datenblattkurven zeigen bei 25 °C spannungsabhängige Leckströme im pA-Bereich, während die Datenblattspezifikation lediglich Leckströme im Bereich von einigen hundert pA garantiert. Ich bin mehr von den Ergebnissen der Kurven bei 25 °C beeindruckt. Die geringen Leckströme wurden bei diesem Gerät offenbar nicht für wichtig genug gehalten, um sie beim Test zu garantieren. Fairerweise muss man sagen, dass die Messung einzelner pA einen hohen technischen Entwicklungsaufwand und lange Testzeiten erfordert.
Bei 85 °C werden einige nA garantiert (die effizient gemessen werden können) mit einem typischen Ergebnis im Bereich von einigen hundert pA. Ich werde diese typischen Ergebnisse als gut akzeptieren.
 Abbildung 16. Simulationsaufbau zur Ermittlung der Leckströme
Die Leckströme sind ein Produktmangel; es gibt diesbezüglich keine genauen Statistiken und sie schwanken stark mit der Temperatur. Es ist nicht die Art von Vorgabe, nach der wir unseren Entwurf ausrichten - vielmehr ist es eine Größe, die die Schaltkreise stört, mit denen der Schalter verbunden ist. Bei der Verwendung von Makromodellen werden sämtliche Leckströme von signifikanter Größe als Schaltungsdefekte simuliert, was eine nützliche Warnung für den Entwickler darstellt. Ich wähle einen Zielwert von 1 nA für einen Schließer bei 85 °C.
Abbildung 16. Simulationsaufbau zur Ermittlung der Leckströme
Die Leckströme sind ein Produktmangel; es gibt diesbezüglich keine genauen Statistiken und sie schwanken stark mit der Temperatur. Es ist nicht die Art von Vorgabe, nach der wir unseren Entwurf ausrichten - vielmehr ist es eine Größe, die die Schaltkreise stört, mit denen der Schalter verbunden ist. Bei der Verwendung von Makromodellen werden sämtliche Leckströme von signifikanter Größe als Schaltungsdefekte simuliert, was eine nützliche Warnung für den Entwickler darstellt. Ich wähle einen Zielwert von 1 nA für einen Schließer bei 85 °C.
 Abbildung 17. Simulationsergebnisse der Leckströme über die Temperatur
Das Modell, das wir hier haben, zeigt keine Leckströme jenseits der Ströme über RCONVERGENCE und GMIN. GMIN ist ein Widerstand, den der Simulator überVerbindungen platziert, um die Konvergenz zu erleichtern. Normalerweise hat dieser einen Leitwert von 1 × 10-12, aber bei Versorgungsspannungen von 30 V können wir ein Vielfaches der Ströme von 30 pA erhalten, was für diese Aufgabe viel zu hoch ist. GMIN wird in daher der Zeile .options der Simulation auf 1 × 10-15 verringert und RCONVERGENCE auf 1 × 1015 erhöht.
Der physikalische Ursprung dieser Leckströme sind vermutlich größtenteils die an jedem Pin angeschlossenen Schutzdioden gegen elektrostatische Entladung (ESD). Wir setzen diese in den Simulationsaufbau in Abbildung 16 ein.'
Nach dem Hantieren mit IS im Diodenmodell erhalten wir die Leckströme über die Temperatur in Abbildung 17.
Logik-Schnittstelle und Gate-Treiber
Eine rein verhaltensbasierte Logic-to-Gate-Treiberschaltung ist in Abbildung 18 dargestellt.
Abbildung 17. Simulationsergebnisse der Leckströme über die Temperatur
Das Modell, das wir hier haben, zeigt keine Leckströme jenseits der Ströme über RCONVERGENCE und GMIN. GMIN ist ein Widerstand, den der Simulator überVerbindungen platziert, um die Konvergenz zu erleichtern. Normalerweise hat dieser einen Leitwert von 1 × 10-12, aber bei Versorgungsspannungen von 30 V können wir ein Vielfaches der Ströme von 30 pA erhalten, was für diese Aufgabe viel zu hoch ist. GMIN wird in daher der Zeile .options der Simulation auf 1 × 10-15 verringert und RCONVERGENCE auf 1 × 1015 erhöht.
Der physikalische Ursprung dieser Leckströme sind vermutlich größtenteils die an jedem Pin angeschlossenen Schutzdioden gegen elektrostatische Entladung (ESD). Wir setzen diese in den Simulationsaufbau in Abbildung 16 ein.'
Nach dem Hantieren mit IS im Diodenmodell erhalten wir die Leckströme über die Temperatur in Abbildung 17.
Logik-Schnittstelle und Gate-Treiber
Eine rein verhaltensbasierte Logic-to-Gate-Treiberschaltung ist in Abbildung 18 dargestellt.
 Abbildung 18. Verhaltensbasierte Logic-to-Gate-Schnittstelle
Der externe Logikeingang befindet sich am In-Anschluss links in Abbildung 18. Es ist der Eingang einer idealen Transkonduktanz Glogic_thresholda, die eine stückweise lineare Übertragungsfunktion hat. Bei Logikeingängen unter 1,37 V beträgt der Ausgang am Logikknoten 0 V; bei Eingängen über 1,43 V liegt logica bei 1 V; und zwischen 1,37 V und 1,43 V bewegt sich logica linear von 0 V auf 1 . Glogic_thresholda ignoriert also Versorgungsspannungsschwankungen, um eine Eingangsschwellenspannung von 1,4 V bereitzustellen.
Cdelaya verlangsamt kurzzeitig den Knoten logica, so dass wir einige Zeitpunkte aus diesem herausgreifen können. Um einen Komparator zu erzeugen, verwenden wir wieder eine Transkonduktanz, hier Gbreakbeforemakena, deren Ausgang wieder von 0 V auf 1 V geht, jedoch mit einem etwas über 0,5 V verschobenen Schwellenwert. Wie in Abbildung 19 zu sehen ist, ermöglichen die verschobenen Abgriffsspannungen 0,52 V und 0,57 V anstelle von 0,5 V ein schnelleres Abschalten von Exponenten, die von 1 V abfallen, als die Einschaltzeit für Exponenten, die von 0 V ansteigen.
Abbildung 18. Verhaltensbasierte Logic-to-Gate-Schnittstelle
Der externe Logikeingang befindet sich am In-Anschluss links in Abbildung 18. Es ist der Eingang einer idealen Transkonduktanz Glogic_thresholda, die eine stückweise lineare Übertragungsfunktion hat. Bei Logikeingängen unter 1,37 V beträgt der Ausgang am Logikknoten 0 V; bei Eingängen über 1,43 V liegt logica bei 1 V; und zwischen 1,37 V und 1,43 V bewegt sich logica linear von 0 V auf 1 . Glogic_thresholda ignoriert also Versorgungsspannungsschwankungen, um eine Eingangsschwellenspannung von 1,4 V bereitzustellen.
Cdelaya verlangsamt kurzzeitig den Knoten logica, so dass wir einige Zeitpunkte aus diesem herausgreifen können. Um einen Komparator zu erzeugen, verwenden wir wieder eine Transkonduktanz, hier Gbreakbeforemakena, deren Ausgang wieder von 0 V auf 1 V geht, jedoch mit einem etwas über 0,5 V verschobenen Schwellenwert. Wie in Abbildung 19 zu sehen ist, ermöglichen die verschobenen Abgriffsspannungen 0,52 V und 0,57 V anstelle von 0,5 V ein schnelleres Abschalten von Exponenten, die von 1 V abfallen, als die Einschaltzeit für Exponenten, die von 0 V ansteigen.
 Abbildung 19. Break before Make-Zeitverhalten.
Die volle Gate-Treiberspannung wird von den Stromquellen mit B_non- und B_pon-Verhalten erzeugt. B_nona liefert einen Strom von VDD/1000, wenn der Knoten n_breakbeforemakena > 0,5 V ist, und treibt die Spannung am Knoten nona auf VDD, da durch einen 1000 Ω-Widerstand belastet.
Wenn der Knoten n_breakbeforemakena < 0,5 V ist, wird der Knoten nona auf VSS gebracht. Damit haben wir einen schönen Rail-to-Rail-Gate-Treiber, der mit den Versorgungsspannungen kompatibel ist und eine feste Eingangsschwelle von 1,4 V hat.
Es gibt noch eine weitere Eigenschaft, die einer Erklärung bedarf. Es ist zu beachten, dass in Abbildung 20 die Verzögerungszeiten durch höhere Versorgungsspannungen verkürzt werden.. Dies wird mittels B_supplysensitivitya implementiert, bei der eine Bruchteil ihres eigenen dynamischen Stroms, der in Abhängigkeit vom VDD variiert, an Cdelaya zurückgeführt wird. An Rsupply_sensitivitya fällt aufgrund des Cdelaya-Stroms nur sehr wenig Spannung ab, so dass sich Cdelaya im Grunde wie ein reiner Kondensator verhält . Das Einspeisen einer Kopie des Stroms von Cdelaya zurück zu Cdelaya erzeugt im Wesentlichen einen steuerbaren variablen Kondensator, und d mathematisch erzeugt Bsupply_sensitivitya die Kurve der Verzögerung in Abhängigkeit von VDD in Abbildung 20.
Abbildung 19. Break before Make-Zeitverhalten.
Die volle Gate-Treiberspannung wird von den Stromquellen mit B_non- und B_pon-Verhalten erzeugt. B_nona liefert einen Strom von VDD/1000, wenn der Knoten n_breakbeforemakena > 0,5 V ist, und treibt die Spannung am Knoten nona auf VDD, da durch einen 1000 Ω-Widerstand belastet.
Wenn der Knoten n_breakbeforemakena < 0,5 V ist, wird der Knoten nona auf VSS gebracht. Damit haben wir einen schönen Rail-to-Rail-Gate-Treiber, der mit den Versorgungsspannungen kompatibel ist und eine feste Eingangsschwelle von 1,4 V hat.
Es gibt noch eine weitere Eigenschaft, die einer Erklärung bedarf. Es ist zu beachten, dass in Abbildung 20 die Verzögerungszeiten durch höhere Versorgungsspannungen verkürzt werden.. Dies wird mittels B_supplysensitivitya implementiert, bei der eine Bruchteil ihres eigenen dynamischen Stroms, der in Abhängigkeit vom VDD variiert, an Cdelaya zurückgeführt wird. An Rsupply_sensitivitya fällt aufgrund des Cdelaya-Stroms nur sehr wenig Spannung ab, so dass sich Cdelaya im Grunde wie ein reiner Kondensator verhält . Das Einspeisen einer Kopie des Stroms von Cdelaya zurück zu Cdelaya erzeugt im Wesentlichen einen steuerbaren variablen Kondensator, und d mathematisch erzeugt Bsupply_sensitivitya die Kurve der Verzögerung in Abhängigkeit von VDD in Abbildung 20.
 Abbildung 20. Ergebnisse für das Break-before-Make-Zeitverhalten aus Simulation und Datenblatt
Nun emuliert unsere Schaltung die TON-Verzögerung als 111 ns für VDD = 4, während die Datenblattkurve 140 ns angibt. Für VDD = 15 V beträgt die simulierte Verzögerung 77 ns gegenüber einer Verzögerung von 60 ns im Datenblatt. Dies ist keine besonders gute Korrelation; ich überlasse es dem Leser, die Funktion Bsupply_sensitivity zu verfeinern, um dies zu verbessern. Immerhin variiert der Break-before-Make-Zeit schön zwischen 15 ns und 24 ns.
Abbildung 20. Ergebnisse für das Break-before-Make-Zeitverhalten aus Simulation und Datenblatt
Nun emuliert unsere Schaltung die TON-Verzögerung als 111 ns für VDD = 4, während die Datenblattkurve 140 ns angibt. Für VDD = 15 V beträgt die simulierte Verzögerung 77 ns gegenüber einer Verzögerung von 60 ns im Datenblatt. Dies ist keine besonders gute Korrelation; ich überlasse es dem Leser, die Funktion Bsupply_sensitivity zu verfeinern, um dies zu verbessern. Immerhin variiert der Break-before-Make-Zeit schön zwischen 15 ns und 24 ns.
 Abbildung 21. Zeitliche Verzögerungen in Abhängigkeit von der Temperatur.
Zwar haben wir nicht viele Datenblattdaten bezüglich der Verzögerung in Abhängigkeit von der Temperatur, aber ich habe einen Temperaturterm zu Cdelaya hinzugefügt, um zumindest die Verlangsamung des Modells im heißen Zustand zu ermöglichen, wie in Abbildung 21 zu sehen ist.
Zusammensetzen des Makromodells
Abbildung 22 zeigt den zusammengesetzten Analogschalter, der zu einem Teilschaltkreis (subcircuit) wird. Anstelle von Parametern wurden harte Zahlen für L und W in die Transistorsymbole eingefügt, und alle Erregungs- und E/A-Signale wurden zugunsten der Pin-Anschlüsse SA, D, SB, In, V , V und Gnd_pin entfernt.
Abbildung 21. Zeitliche Verzögerungen in Abhängigkeit von der Temperatur.
Zwar haben wir nicht viele Datenblattdaten bezüglich der Verzögerung in Abhängigkeit von der Temperatur, aber ich habe einen Temperaturterm zu Cdelaya hinzugefügt, um zumindest die Verlangsamung des Modells im heißen Zustand zu ermöglichen, wie in Abbildung 21 zu sehen ist.
Zusammensetzen des Makromodells
Abbildung 22 zeigt den zusammengesetzten Analogschalter, der zu einem Teilschaltkreis (subcircuit) wird. Anstelle von Parametern wurden harte Zahlen für L und W in die Transistorsymbole eingefügt, und alle Erregungs- und E/A-Signale wurden zugunsten der Pin-Anschlüsse SA, D, SB, In, V , V und Gnd_pin entfernt.
 Abbildung 22. Zusammengesetzte SPDT-Teilschaltung spdt 40V.asc.
Eine zweite Logikschnittstelle ist für den anderen Schalter des spdt-Paars vorgesehen. ESD-Schutzdioden sind zwischen den analogen Anschlüssen und VSS sowie zwischen dem logischen Eingang und Masse installiert. Zu beachten ist, dass das Suffix „-a" in den Namen der oberen Bausteine und Knoten der Logikschnittstelle als Suffix „-b“ in der unteren Schnittstelle repliziert wird. Die Schnittstelle Glogic_thresholdb hat den entgegengesetzten Ausgang aus der Tabelle in Glogic_ thresholda, damit das eine oder andere Schalterpaar arbeiten kann, anstatt gleichzeitig eingeschaltet zu werden.
Abbildung 22. Zusammengesetzte SPDT-Teilschaltung spdt 40V.asc.
Eine zweite Logikschnittstelle ist für den anderen Schalter des spdt-Paars vorgesehen. ESD-Schutzdioden sind zwischen den analogen Anschlüssen und VSS sowie zwischen dem logischen Eingang und Masse installiert. Zu beachten ist, dass das Suffix „-a" in den Namen der oberen Bausteine und Knoten der Logikschnittstelle als Suffix „-b“ in der unteren Schnittstelle repliziert wird. Die Schnittstelle Glogic_thresholdb hat den entgegengesetzten Ausgang aus der Tabelle in Glogic_ thresholda, damit das eine oder andere Schalterpaar arbeiten kann, anstatt gleichzeitig eingeschaltet zu werden.
 Abbildung 23. Schaltbild des Makromodells für den ADG333A
Ein alternatives ESD-Schutzkonzept umfasst Dioden von einem geschützten Pin zu sowohl VDD als auch zu VSS sowie eine Klemme zwischen VDD und VSS. Das Datenblatt liefert im Allgemeinen einen Einblick bezüglich des Schutzkonzepts, und Leckströme werden beiden Versorgungen zugeordnet.
Die Teilschaltung „spdt“ wird mit einem Symbol versehen und im Masterschaltbild ADG333A.asc von Abbildung 23 viermal verwendet.
Abbildung 24 ist das Schaltbild des Prüfaufbaus zur Verifizierung der endgültigen Makromodell-Ergebnisse.
Abbildung 23. Schaltbild des Makromodells für den ADG333A
Ein alternatives ESD-Schutzkonzept umfasst Dioden von einem geschützten Pin zu sowohl VDD als auch zu VSS sowie eine Klemme zwischen VDD und VSS. Das Datenblatt liefert im Allgemeinen einen Einblick bezüglich des Schutzkonzepts, und Leckströme werden beiden Versorgungen zugeordnet.
Die Teilschaltung „spdt“ wird mit einem Symbol versehen und im Masterschaltbild ADG333A.asc von Abbildung 23 viermal verwendet.
Abbildung 24 ist das Schaltbild des Prüfaufbaus zur Verifizierung der endgültigen Makromodell-Ergebnisse.
 Abbildung 24. Prüfaufbau für das ADG333A-Makromodell
Zusammenfassung
Wir haben gesehen, wie sich ein ordentliches Makromodell für einen bestimmten Analogschalter realisieren lässt und wie man Parameter erhält, die ein paar verschiedene Halbleiterprozesse unterstützen, die zur Realisierung des physikalischen Bauteils verwendet werden. Das resultierende Makromodell zeigt Mängel auf, wie beispielsweise bezüglich des On-Widerstands und dessen Schwankungen, der Ladungsinjektion als Funktion des Versorgungs- und Signalspannungspegels, der parasitären Kapazitäten und deren Schwankungen über der Spannung, Verzögerungen der Logikschnittstelle und Leckströme. Wir hoffen, dass die Makromodelle bei der Simulation de tatsächlichen Verhaltensmerkmale von Analogschaltern hilfreich sind.
Nachtrag
Um LTspice herunterzuladen, besuchen Sie bitte analog.com/ltspice.
Hier ist die LTspice-Textdatei des Makromodell-Symbols, die unter dem Namen ADG333.asy gespeichert wird. Sie enthält Einzelheiten zur Simulation der Teilschaltung. Anstatt den Schema für ADG333.asc in jeden Schaltplan zu kopieren, der dieses Bauteil verwendet, verwenden wir ein Symbol, das darauf als .asy verweist. Innerhalb des ADG333-Symbols befinden sich einzelne Schaltersymbole. Dies ist das Symbol des Simulationsinhalts, das als spdt_40V.asc gespeichert wird. Das eigentliche Symbol wird als spdt_40V.asy gespeichert.
Abbildung 24. Prüfaufbau für das ADG333A-Makromodell
Zusammenfassung
Wir haben gesehen, wie sich ein ordentliches Makromodell für einen bestimmten Analogschalter realisieren lässt und wie man Parameter erhält, die ein paar verschiedene Halbleiterprozesse unterstützen, die zur Realisierung des physikalischen Bauteils verwendet werden. Das resultierende Makromodell zeigt Mängel auf, wie beispielsweise bezüglich des On-Widerstands und dessen Schwankungen, der Ladungsinjektion als Funktion des Versorgungs- und Signalspannungspegels, der parasitären Kapazitäten und deren Schwankungen über der Spannung, Verzögerungen der Logikschnittstelle und Leckströme. Wir hoffen, dass die Makromodelle bei der Simulation de tatsächlichen Verhaltensmerkmale von Analogschaltern hilfreich sind.
Nachtrag
Um LTspice herunterzuladen, besuchen Sie bitte analog.com/ltspice.
Hier ist die LTspice-Textdatei des Makromodell-Symbols, die unter dem Namen ADG333.asy gespeichert wird. Sie enthält Einzelheiten zur Simulation der Teilschaltung. Anstatt den Schema für ADG333.asc in jeden Schaltplan zu kopieren, der dieses Bauteil verwendet, verwenden wir ein Symbol, das darauf als .asy verweist. Innerhalb des ADG333-Symbols befinden sich einzelne Schaltersymbole. Dies ist das Symbol des Simulationsinhalts, das als spdt_40V.asc gespeichert wird. Das eigentliche Symbol wird als spdt_40V.asy gespeichert.Über den Autor: Barry Harvey hat als Entwickler für Analog ICs gearbeitet und Hochgeschwindigkeits-Operationsverstärker, Spannungsreferenzen, Mixed-Signal-Schaltungen, Videoschaltungen, DSL-Leitungstreiber, DACs, Sample-and-Hold-Verstärker, Multipliziere und vieles mehr entworfen. Er hat einen Masterabschluss in Elektrotechnik (MSEE) von der Universität Stanford. Er ist Inhaber von mehr als 20 Patenten und hat ungefähr ebenso viele Artikel und Arbeiten veröffentlicht. Er ist zu erreichen unter barry.harvey@analog.com. / Copyright: © Analog Devices Inc.





